题目内容
设数列{an}中,a1=2,an+1=an+n+1,则通项an= .
【答案】分析:根据数列的递推式,依次写出n=1,2,3…n的数列相邻两项的关系,进而格式相加即可求得答案.
解答:解:∵a1=2,an+1=an+n+1
∴an=an-1+(n-1)+1,an-1=an-2+(n-2)+1,an-2=an-3+(n-3)+1,…,a3=a2+2+1,a2=a1+1+1,a1=2=1+1
将以上各式相加得:an=[(n-1)+(n-2)+(n-3)++2+1]+n+1
=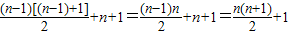
故答案为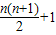 ;
;
点评:此题重点考查由数列的递推公式求数列的通项公式.重视递推公式的特征与解法的选择;抓住an+1=an+n+1中an+1,an系数相同是找到方法的突破口;此题可用累和法,迭代法等;
解答:解:∵a1=2,an+1=an+n+1
∴an=an-1+(n-1)+1,an-1=an-2+(n-2)+1,an-2=an-3+(n-3)+1,…,a3=a2+2+1,a2=a1+1+1,a1=2=1+1
将以上各式相加得:an=[(n-1)+(n-2)+(n-3)++2+1]+n+1
=
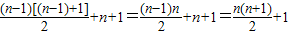
故答案为
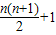 ;
;点评:此题重点考查由数列的递推公式求数列的通项公式.重视递推公式的特征与解法的选择;抓住an+1=an+n+1中an+1,an系数相同是找到方法的突破口;此题可用累和法,迭代法等;

练习册系列答案
相关题目