题目内容
10.函数f(x)=sinxsin(x+$\frac{π}{3}$)+sin2x,x∈(-$\frac{π}{2}$,$\frac{π}{4}$)的值域为[$\frac{3-2\sqrt{3}}{4}$,$\frac{3+2\sqrt{3}}{4}$].分析 化简可得f(x)=$\frac{3}{4}$+$\frac{\sqrt{3}}{2}$sin(2x-$\frac{π}{3}$),由三角函数的知识可得值域.
解答 解:化简可得f(x)=sinxsin(x+$\frac{π}{3}$)+sin2x
=sinx($\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx)+sin2x
=$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$sinxcosx+sin2x
=$\frac{3}{2}$•$\frac{1-cos2x}{2}$+$\frac{\sqrt{3}}{4}$sin2x
=$\frac{3}{4}$+$\frac{\sqrt{3}}{4}$sin2x-$\frac{3}{4}$cos2x
=$\frac{3}{4}$+$\frac{\sqrt{3}}{2}$($\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x)
=$\frac{3}{4}$+$\frac{\sqrt{3}}{2}$sin(2x-$\frac{π}{3}$),
∴函数的值域为[$\frac{3-2\sqrt{3}}{4}$,$\frac{3+2\sqrt{3}}{4}$],
故答案为:[$\frac{3-2\sqrt{3}}{4}$,$\frac{3+2\sqrt{3}}{4}$].
点评 本题考查三角函数恒等变换,涉及三角函数的值域,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知直线l经过椭圆$\frac{x^2}{169}$+$\frac{y^2}{144}$=1的右焦点,与椭圆交于A(x1,y1)、B(x2,y2),若x1+x2=1,则直线l的方程为( )
| A. | 4x-13y-20=0或4x+13y-20=0 | B. | 2x-3y-10=0或2x+3y-10=0 | ||
| C. | 6x+5y-30=0或6x-5y-30=0 | D. | 4x+9y-20=0或2x+3y-10=0. |
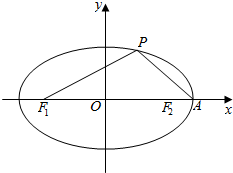 如图,椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左、右两个焦点分别为F1、F2,A为椭圆的右顶点,点P在椭圆上且∠PF1F2=arccos$\frac{7}{8}$
如图,椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左、右两个焦点分别为F1、F2,A为椭圆的右顶点,点P在椭圆上且∠PF1F2=arccos$\frac{7}{8}$