题目内容
1.在平面内有下面关于直角三角形边长的勾股定理定理:直角三角形ABC中,AC⊥BC,则有AB2=AC2+BC2.将它类比到空间中关于直角三棱锥的面积的命题应该是:若三棱锥P-ABC中,PA⊥PB,PB⊥PC,PC⊥PA;则有${{S}^{2}}_{△ABC}={{S}^{2}}_{△PAB}+{{S}^{2}}_{△PBC}+{{S}^{2}}_{△PCA}$.分析 斜边的平方等于两个直角边的平方和,可类比到空间就是斜面面积的平方等于三个直角面的面积的平方和,边对应着面.
解答 解:由边对应着面,边长对应着面积,由类比可得
${S^2}_{△ABC}={S^2}_{△PAB}+{S^2}_{△PBC}+{S^2}_{△PCA}$.
故答案为:${{S}^{2}}_{△ABC}={{S}^{2}}_{△PAB}+{{S}^{2}}_{△PBC}+{{S}^{2}}_{△PCA}$.
点评 本题考查了从平面类比到空间,属于基本类比推理.利用类比推理可以得到结论、证明类比结论时证明过程与其类比对象的证明过程类似或直接转化为类比对象的结论.

练习册系列答案
相关题目
11.已知x,y满足$\left\{\begin{array}{l}{x+y-2≤0}\\{x-y+1≥0}\\{x+2y-2≥0}\end{array}\right.$,若z=3x-2y的最大值为a,最小值为b,则ab=( )
| A. | -12 | B. | -9 | C. | 3 | D. | 6 |
16.下列函数既是偶函数,又在(0,+∞)上单调递增的是( )
| A. | y=-x2 | B. | y=x3 | C. | y=log2|x| | D. | y=-3-x |
13.下列函数中,既是偶函数又在(0,+∞)上是增函数的是( )
| A. | $y={x^{\frac{2}{3}}}$ | B. | $y={x^{\frac{3}{2}}}$ | C. | y=x-2 | D. | $y={x^{-\frac{1}{2}}}$ |
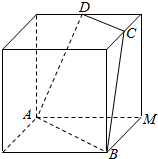 如图所示,正方体的棱长为2,C、D分别是两条棱的中点,A、B、M是顶点,那么M到截面ABCD的距离是$\frac{4}{3}$.
如图所示,正方体的棱长为2,C、D分别是两条棱的中点,A、B、M是顶点,那么M到截面ABCD的距离是$\frac{4}{3}$.