题目内容
2.已知函数f(x)=ex-kx,x∈R(1)若k=e,试确定函数f(x)的单调区间;
(2)讨论f(x)的极值.
分析 (1)求出f′(x)=ex-e.利用导函数的符号,求解函数的单调区间即可.
(2)f′(x)=ex-k,通过①k≤0时,②当k>0时,利用导函数的符号,判断函数的单调性以及极值即可.
解答 解:(1)由k=e 得f(x)=ex-ex,所以f′(x)=ex-e.
由f′(x)>0 得x>1,故f(x)的单调递增区间是(1,+∞),
由f′(x)<0 得x<1,故f(x)的单调递减区间是(-∞,1).…4分
(2)f′(x)=ex-k,
①k≤0时,f′(x)>0 对x∈R恒成立,
所以此时f(x)在(-∞,+∞) 上单调递增,无极值; …..…6分
②当k>0时,f′(x)=ex-k=0 得x=lnk.
当x 变化时f′(x),f(x)的变化情况如下表:
| x | (-∞,lnk) | Lnk | (lnk,+∞) |
| f’(x) | - | 0 | + |
| f(x) | 单调递减 | 极小值 | 单调递增 |
点评 本题考查函数的导数的综合应用,函数的极值以及函数的单调性的应用,考查分类讨论思想以及转化思想的应用,考查计算能力.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
12.已知f(x)是定义在R上的可导函数,当x∈(1,+∞)时,(x-1)f′(x)-f(x)>0恒成立,若a=f(2),b=$\frac{1}{2}$f(3),c=$\frac{1}{{\sqrt{2}-1}}f(\sqrt{2})$,则a,b,c的大小关系是( )
| A. | c<a<b | B. | a<b<c | C. | b<a<c | D. | a<c<b |
13.函数f(x)=(x-3)ex的单调增区间是( )
| A. | (-∞,2) | B. | (2,+∞) | C. | (1,4) | D. | (0,3) |
17.若定义在R上的可导函数f(x)的导函数为f′(x),在R上满足f′(x)>f(x),且y=f(x-3)为奇函数,f(-6)=-3,则不等式f(x)<3ex的解集为( )
| A. | (0,+∞) | B. | (-3,+∞) | C. | (-∞,0) | D. | (-∞,6) |
7.在极坐标系中,圆心为(2,$\frac{π}{4}$),半径为1的圆的极坐标方程是( )
| A. | ρ=8sin(θ-$\frac{π}{4}$) | B. | ρ=8cos(θ-$\frac{π}{4}$) | ||
| C. | ρ2-4ρcos(θ-$\frac{π}{4}$)+3=0 | D. | ρ2-4ρsin(θ-$\frac{π}{4}$)+3=0 |
11.函数f(x)=$\sqrt{3}$x+2cosx,x∈(0,π)上单调减区间为( )
| A. | ($\frac{π}{3}$,$\frac{2π}{3}$) | B. | ($\frac{π}{6}$,$\frac{5π}{6}$) | C. | (0,$\frac{π}{3}$),($\frac{2π}{3}$,π) | D. | (0,$\frac{π}{6}$),($\frac{5π}{6}$,π) |
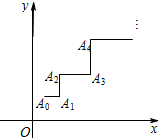 一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图,A0(x0,y0)的坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.
一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图,A0(x0,y0)的坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.