题目内容
已知函数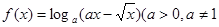 为常数).
为常数).
(Ⅰ)求函数 的定义域;
的定义域;
(Ⅱ)若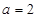 ,
,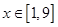 ,求函数
,求函数 的值域;
的值域;
(Ⅲ)若函数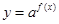 的图像恒在直线
的图像恒在直线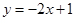 的上方,求实数
的上方,求实数 的取值范围.
的取值范围.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)
;(Ⅲ) 且
且
解析试题分析:(1)对数中真数大于0(2)思路:要先求真数的范围再求对数的范围。求真数范围时用配方法,求对数范围时用点调性(3)要使函数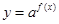 的图像恒在直线
的图像恒在直线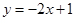 的上方,则有
的上方,则有  在
在 上恒成立。把
上恒成立。把 看成整体,令
看成整体,令 即
即 在
在 上恒成立,转化成单调性求最值问题
上恒成立,转化成单调性求最值问题
试题解析:(Ⅰ)







 所以定义域为
所以定义域为
(Ⅱ)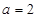 时
时  令
令 则
则
因为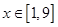 所以
所以 ,所以
,所以 即
即
所以函数 的值域为
的值域为
(Ⅲ)
要使函数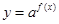 的图像恒在直线
的图像恒在直线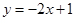 的上方
的上方
则有  在
在 上恒成立。 令
上恒成立。 令 则
则
即 在
在 上恒成立
上恒成立 的图像的对称轴为
的图像的对称轴为 且
且
所以 在
在 上单调递增,要想
上单调递增,要想 恒成立,只需
恒成立,只需
即



因为 且
且 所以
所以  且
且
考点:(1)对数的定义域(2)对数的单调性(3)恒成立问题

练习册系列答案
相关题目
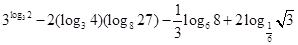 .
.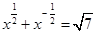 ,求
,求 的值.
的值.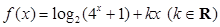 是偶函数。
是偶函数。 的值;
的值;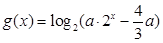 ,其中实数
,其中实数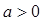 。若函数
。若函数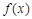 与
与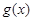 的图象有且只有一个交点,求实数
的图象有且只有一个交点,求实数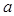 的取值范围。
的取值范围。 ,h(x)=2alnx,
,h(x)=2alnx,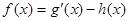 .
. 的单调性;
的单调性;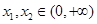 ,且
,且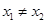 ,都有
,都有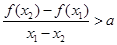
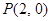 ,点
,点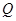 在曲线
在曲线 :
: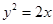 上.
上.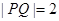 ,求点
,求点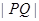 的最小值.
的最小值.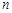 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图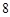 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为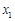 ,
,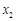 ,
,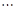 ,
,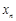 ,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.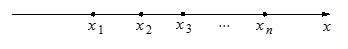
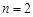 ,每个工作台上只有一名工人,试确定供应站的位置;
,每个工作台上只有一名工人,试确定供应站的位置;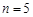 ,工作台从左到右的人数依次为
,工作台从左到右的人数依次为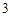 ,
,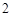 ,
,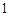 ,
,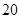 年的隔热层,每厘米厚的隔热层建造成本为
年的隔热层,每厘米厚的隔热层建造成本为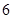 万元.该建筑物每年的能源消耗费用
万元.该建筑物每年的能源消耗费用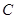 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度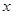 (单位:
(单位: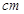 )满足关系:
)满足关系: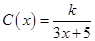 (
(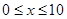 ,
, 为常数),若不建隔热层,每年能源消耗费用为
为常数),若不建隔热层,每年能源消耗费用为 万元.设
万元.设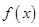 为隔热层建造费用与
为隔热层建造费用与 是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛
是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛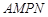 ,要求:B在
,要求:B在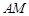 上,D在
上,D在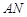 上,对角线
上,对角线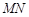 过C点,且矩形
过C点,且矩形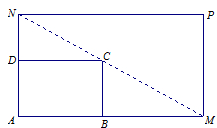
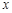 米,矩形
米,矩形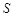 平方米,试用解析式将
平方米,试用解析式将