题目内容
为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用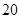 年的隔热层,每厘米厚的隔热层建造成本为
年的隔热层,每厘米厚的隔热层建造成本为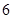 万元.该建筑物每年的能源消耗费用
万元.该建筑物每年的能源消耗费用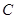 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度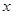 (单位:
(单位: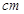 )满足关系:
)满足关系: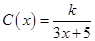 (
(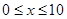 ,
, 为常数),若不建隔热层,每年能源消耗费用为
为常数),若不建隔热层,每年能源消耗费用为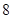 万元.设
万元.设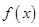 为隔热层建造费用与
为隔热层建造费用与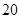 年的能源消耗费用之和.
年的能源消耗费用之和.
(1)求 的值及
的值及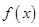 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用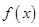 达到最小,并求最小值.
达到最小,并求最小值.
(1)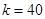 ,
,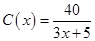 ;
;
(2)隔热层修建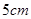 厚时,总费用
厚时,总费用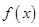 达到最小,最小值为
达到最小,最小值为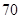 万元.
万元.
解析试题分析:(1)先从题干条件“不建隔热层,每年能源消耗费用为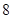 万元”这一条件中得到
万元”这一条件中得到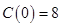 ,进而求出
,进而求出 的值,然后利用函数
的值,然后利用函数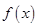 的定义求出函数
的定义求出函数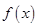 的解析式;(2)将函数
的解析式;(2)将函数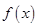 的解析式进行陪凑,凑成
的解析式进行陪凑,凑成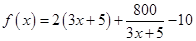 ,然后利用基本不等式求出
,然后利用基本不等式求出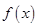 的最小值,有等号成立的条件求出相应的
的最小值,有等号成立的条件求出相应的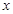 值,从而使问题得到解答.
值,从而使问题得到解答.
试题解析:(1)当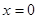 时,
时,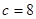 ,
,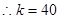 ,
,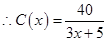 ,
,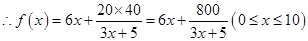 ,
,
(2)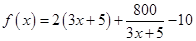 ,
,
设 ,
,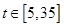 ,
,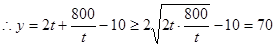 .
.
当且仅当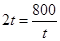 ,即
,即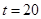 时等号成立,这时
时等号成立,这时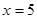 ,因此
,因此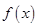 的最小值为
的最小值为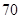 .
.
即隔热层修建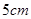 厚时,总费用
厚时,总费用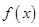 达到最小,最小值为
达到最小,最小值为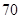 万元.
万元.
考点:1.函数的解析式;2.基本不等式

练习册系列答案
相关题目
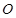 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 米,圆心角为
米,圆心角为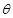 (弧度).
(弧度).
 ,求
,求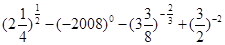
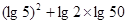
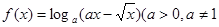 为常数).
为常数). 的定义域;
的定义域;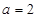 ,
,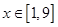 ,求函数
,求函数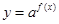 的图像恒在直线
的图像恒在直线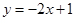 的上方,求实数
的上方,求实数 的取值范围.
的取值范围.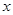 万件(假设该厂生产的产品全部销售),与年促销费用
万件(假设该厂生产的产品全部销售),与年促销费用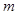 万元
万元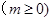 近似满足
近似满足 ,如果不促销,该产品的年销售量只能是1万件.已知2013年生产该产品的固定投入10万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格规定为每件产品成本的1.5倍.(产品成本包括固定投入和再投入两部分资金).
,如果不促销,该产品的年销售量只能是1万件.已知2013年生产该产品的固定投入10万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格规定为每件产品成本的1.5倍.(产品成本包括固定投入和再投入两部分资金).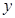 万元表示为年促销费用
万元表示为年促销费用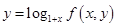 ,
, ,
,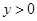 .
.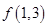 与
与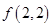 的大小;
的大小; ,证明:
,证明: ;
;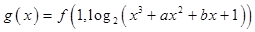 的图象为曲线
的图象为曲线 ,曲线
,曲线 处的切线斜率为
处的切线斜率为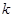 ,若
,若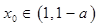 ,且存在实数
,且存在实数 ,使得
,使得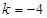 ,求实数
,求实数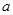 的取值范围.
的取值范围.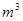 ,如果每年平均增长5﹪,经过
,如果每年平均增长5﹪,经过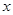 年,树林中有木材
年,树林中有木材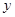
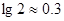 ,
,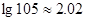 )
) 元,
元,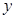 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格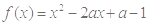 在区间[0,1]上有最小值-2,求
在区间[0,1]上有最小值-2,求 的值.
的值.