题目内容
已知函数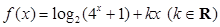 是偶函数。
是偶函数。
(1)求 的值;
的值;
(2)设函数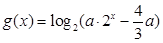 ,其中实数
,其中实数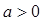 。若函数
。若函数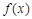 与
与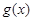 的图象有且只有一个交点,求实数
的图象有且只有一个交点,求实数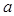 的取值范围。
的取值范围。
(1)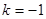 ;(2)
;(2)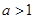
解析试题分析:(1)根据偶函数定义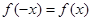 可得到关于k的方程,根据对应系数相等可解出k的值。(2)由题意分析可知将函数
可得到关于k的方程,根据对应系数相等可解出k的值。(2)由题意分析可知将函数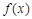 与
与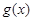 的图象有且只有一个交点的问题 为方程
的图象有且只有一个交点的问题 为方程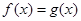 只有一个根的问题。将
只有一个根的问题。将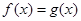 整理变形并结合换元法可转化为
整理变形并结合换元法可转化为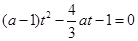 ,在
,在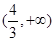 上只有一个解的问题。因为此二次函数对称轴是变量,属于动轴定区间问题。分情况讨论,详见解析。
上只有一个解的问题。因为此二次函数对称轴是变量,属于动轴定区间问题。分情况讨论,详见解析。
试题解析:解:(1)∵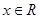 由题有
由题有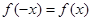 对
对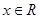 恒成立 …2分
恒成立 …2分
即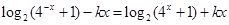 恒成立,整理得
恒成立,整理得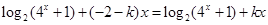 ,所以
,所以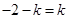 ∴
∴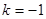
(2)由函数的定义域得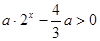 , 由于
, 由于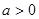
所以 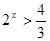 即定义域为
即定义域为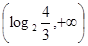
∵函数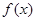 与
与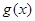 的图象有且只有一个交点,即方程
的图象有且只有一个交点,即方程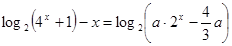 在
在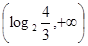 上只有一解。
上只有一解。
即:方程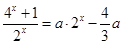 在
在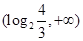 上只有一解
上只有一解
令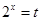 ,则
,则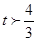 ,上式可变形为
,上式可变形为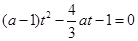 ,在
,在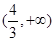 上只有一个解。
上只有一个解。
当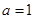 时,
时, 舍。
舍。
当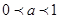 时,记
时,记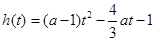 ,其图像的对称轴为
,其图像的对称轴为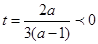 ,所以
,所以 在
在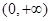 上单调递减,而
上单调递减,而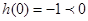 。所以方程
。所以方程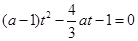 在
在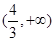 上无解。
上无解。
当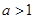 时,记
时,记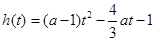 ,其图象的对称轴
,其图象的对称轴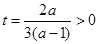
所以只需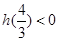 ,即
,即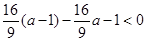 ,此恒成立
,此恒成立
∴此时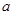 的范围为
的范围为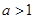
综上所述,所求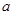 的取值范围为
的取值范围为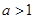
考点:奇偶性,数形结合思想,二次函数的动轴定区间问题

练习册系列答案
相关题目
 ,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).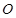 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 米,圆心角为
米,圆心角为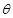 (弧度).
(弧度).
 ,求
,求 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是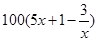 元.
元.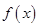 的自变量的取值区间为A,若其值域区间也为A,则称A为
的自变量的取值区间为A,若其值域区间也为A,则称A为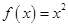 形如
形如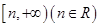 的保值区间;
的保值区间;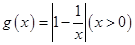 是否存在形如
是否存在形如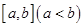 的保值区间?若存在,求出实数
的保值区间?若存在,求出实数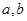 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.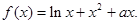
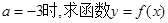 的极值点;
的极值点;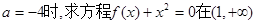 上的根的个数.
上的根的个数.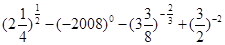
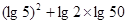
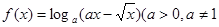 为常数).
为常数). 的定义域;
的定义域;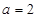 ,
,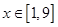 ,求函数
,求函数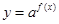 的图像恒在直线
的图像恒在直线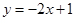 的上方,求实数
的上方,求实数 的取值范围.
的取值范围. 元,
元,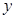 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格