题目内容

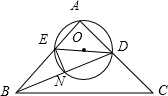如图，在等腰△ABC中，AB=AC，D是AC的中点，DE平分∠ADB，交AB于E，过A，D，E的圆交BD于N，若AE=
3
2
，则BN=
 
．
考点：与圆有关的比例线段
专题：立体几何
分析：设BE=x，则AB=x+
3
2
，AD=
1
2
AB=
2x+3
4
，由已知得△BEN∽△BDA，由此得到x=3，BE=3，AB=
9
2
，AD=
9
4
，再由△BEN∽△BDA，得
BN
AB
=
EN
AD
，由此能求出BN．
解答： 解：设BE=x，则AB=x+
3
2
，AD=
1
2
AB=
2x+3
4
，
∵∠BEN=∠ADB，∠BNE=∠BAD，
∴△BEN∽△BDA，∴
BE
AB
=
EN
AD
=
BN
BD
，
∵DE平分∠ADB，交AB于E，∴EN=AE=
3
2
，
∴
x
x+
3
2
=
3
2
2x+3
4
，解得x=3，∴BE=3，AB=
9
2
，AD=
9
4
，
∵△BEN∽△BDA，∴
BN
AB
=
EN
AD
，
∴BN=
AB•EN
AD
=
9
2
×
3
2
9
4
=3．
故答案为：3．
点评：本题考查与圆有关的线段长的求法，是中档题，解题时要注意圆的简单性质和三角形相似的性质的合理运用．
练习册系列答案
相关题目
设{an}是由正数组成的等比数列，Sn为其前n项和．已知a2a4=1，S3=7，则S5=（　　）
A、
15
2
B、
17
2
C、
31
4
D、
33
4
已知数列{an}的前n项和为Sn，a1=1，an≠0，anan+1=4Sn-1
（1）求数列{an}的通项公式；
（2）设bn=
1
anan+1
，求数列{bn}的前n项和Tn．
设球的表面积为S1，体积为V1．它的内接正方体的表面积为S2，体积为V2，求S1：S2，V1：V2．
已知0＜a≤2，且函数f（x）=cos2x-asinx+b的最大值为0，最小值为-4，求a，b．
已知：两圆C1：x2+y2+4x-6y+12=0，C2：x2+y2-2x-14y+k=0．
（1）实数k为何值时，两圆相交；
（2）实数k为何值时，两圆相切；
（3）实数k为何值时，两圆相离．
若变量x、y满足约束条件
x-y+1≥0
x+y-1≥0
x-2≤0
，则z=2x+y的最大值是（　　）
A、-2B、1C、3D、7
在锐角三角形ABC中，a，b，c分别为内角A，B，C所对的边，且满足
3
a-2bsinA=0．
（1）求角B的大小；
（2）当△ABC的外接圆的面积为4π时，求△ABC面积的最大值．
从1至9的9个自然数中任取2个数，分别作为对数的底数和真数，共可得到多少不同的对数值？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网