题目内容
已知向量
，
，
满足
=
+
．
（Ⅰ）若
=（3，1），
=（1，y），
∥
，求实数y的值；
（Ⅱ）若|
|=2|
|≠0，
⊥
，求向量
，
的夹角θ．
| a |
| b |
| c |
| c |
| a |
| b |
（Ⅰ）若
| a |
| b |
| a |
| c |
（Ⅱ）若|
| b |
| a |
| a |
| c |
| a |
| b |
考点：平面向量数量积的坐标表示、模、夹角,平面向量数量积的运算
专题：平面向量及应用
分析：（Ⅰ）由
、
，求出
，再由
∥
，求出y的值；
（Ⅱ）由
⊥
，得
•
=0，由|
|=2|
|≠0，求出cosθ的值，从而得出夹角θ的值．
| a |
| b |
| c |
| a |
| c |
（Ⅱ）由
| a |
| c |
| a |
| c |
| b |
| a |
解答：
解：（Ⅰ）∵
=
+
，
=（3，1），
=（1，y），
∴
=（4，1+y）；（2分）
又∵
∥
，
∴3（1+y）-4×1=0，（4分）
解得y=
；（6分）
（Ⅱ）∵
=
+
，且
⊥
，
∴
•
=
•（
+
）=
2+
•
=0，
即
•
=-
2；（9分）
又∵|
|=2|
|≠0，
∴cosθ=
=
=-
；（11分）
∵θ∈[0，π]，
∴θ=
．（13分）
| c |
| a |
| b |
| a |
| b |
∴
| c |
又∵
| a |
| c |
∴3（1+y）-4×1=0，（4分）
解得y=
| 1 |
| 3 |
（Ⅱ）∵
| c |
| a |
| b |
| a |
| c |
∴
| a |
| c |
| a |
| a |
| b |
| a |
| a |
| b |
即
| a |
| b |
| a |
又∵|
| b |
| a |
∴cosθ=
| ||||
|
|
-|
| ||
2|
|
| 1 |
| 2 |
∵θ∈[0，π]，
∴θ=
| 2π |
| 3 |
点评：本题考查了平面向量的应用问题，解题时应用向量的数量积判定垂直与平行以及求夹角问题，是基础题．
练习册系列答案
初中学业考试导与练系列答案
相关题目
若实数a、b满足a+b=1，则3a+3b的最小值是（ ）
| A、18 | |||
B、2
| |||
| C、6 | |||
D、2
|
设全集U=Z，A={-1，0，1，2}，B{x|x2-2x=0}，则A∩∁UB为（ ）
| A、{2} |
| B、{-1，0，1} |
| C、{0，2} |
| D、{-1，1} |
在一项科学实验中，要先后实施5个程序，程序A和B在实施时必须相邻，问实验顺序的编排方法共有（ ）种．
| A、24种 | B、48种 |
| C、60种 | D、120种 |
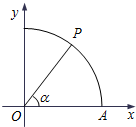如图，曲线Γ：x2+y2=1（x≥0，y≥0）与x轴交于点A，点P在曲线Γ上，∠AOP=α．