题目内容
2.设函数f(x)=xea-x+bx,曲线y=f(x)在点(2,f(2))处的切线方程为y=(e-1)x+4.(1)求a,b的值;
(2)求f(x)的单调区间.
分析 (1)求函数的导数,根据导数的几何意义求出函数的切线斜率以及f(2),建立方程组关系即可求a,b的值;
(2)求函数的导数,利用函数单调性和导数之间的关系即可求f(x)的单调区间.
解答 解:(1)∵y=f(x)在点(2,f(2))处的切线方程为y=(e-1)x+4,
∴当x=2时,y=2(e-1)+4=2e+2,即f(2)=2e+2,
同时f′(2)=e-1,
∵f(x)=xea-x+bx,
∴f′(x)=ea-x-xea-x+b,
则$\left\{\begin{array}{l}{f(2)=2{e}^{a-2}+2b=2e+2}\\{f′(2)={e}^{a-2}-2{e}^{a-2}+b=e-1}\end{array}\right.$,
即a=2,b=e;
(2)∵a=2,b=e;
∴f(x)=xe2-x+ex,
∴f′(x)=e2-x-xe2-x+e=(1-x)e2-x+e,
f″(x)=-e2-x-(1-x)e2-x=(x-2)e2-x,
由f″(x)>0得x>2,由f″(x)<0得x<2,
即当x=2时,f′(x)取得极小值f′(2)=(1-2)e2-2+e=e-1>0,
∴f′(x)>0恒成立,
即函数f(x)是增函数,
即f(x)的单调区间是(-∞,+∞).
点评 本题主要考查导数的应用,根据导数的几何意义,结合切线斜率建立方程关系以及利用函数单调性和导数之间的关系是解决本题的关键.综合性较强.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
1.在直角坐标平面内,曲线|x-1|+|x+1|+|y|=4围成的图形面积为( )
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
10.已知a=0.40.4,b=1.20.4,c=log20.4,则a,b,c的大小关系为( )
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | a<c<b |
17.已知函数$f(x)=\left\{\begin{array}{l}x+1(x<1)\\-x+3(x≥1)\end{array}\right.$,则$f[f(\frac{5}{2})]$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{9}{2}$ | D. | $\frac{3}{2}$ |
7.已知命题p:?x0∈R,x0-2>0,命题q:?x∈R,$\sqrt{x}$<x,则下列说法中正确的是( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |
11.已知集合M={x|x2-2x-8≤0},集合N={x|lgx≥0},则M∩N=( )
| A. | {x|x≥4} | B. | {x|1≤x≤4} | C. | {x|x≥1} | D. | {x|x≥-2} |
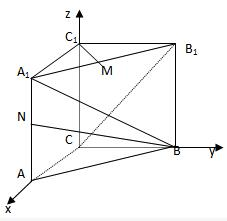 如图所示,直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
如图所示,直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.