题目内容
10. 如图,已知F1,F2是椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,若点Q为线段PF2的中点,则b的值为( )
如图,已知F1,F2是椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,若点Q为线段PF2的中点,则b的值为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 2$\sqrt{2}$ |
分析 通过画出草图,连结OQ可知OQ⊥PF2且|OQ|=b,进而可知OQ是三角形PF1F2的中位线,利用勾股定理计算即得结论.
解答 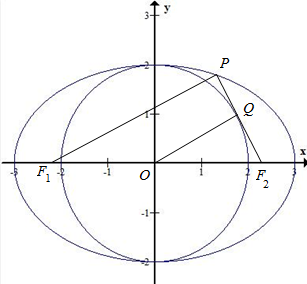 解:连结OQ,如图,
解:连结OQ,如图,
∵线段PF2与圆x2+y2=b2相切于点Q,
∴OQ⊥PF2,且|OQ|=b,
又∵点Q为线段PF2的中点,
∴直线OQ是线段PF2的中垂线,
又∵点O是F1F2的中点,
∴OQ是三角形PF1F2的中位线,
∴|PF1|=2|OQ|=2b,
由椭圆定义可知|QF2|=$\frac{2×\sqrt{9}-2b}{2}$=3-b,|OF2|=$\sqrt{9-{b}^{2}}$,
根据勾股定理可知:9-b2=b2+(3-b)2,
解得:b=2,
故选:B.
点评 本题考查椭圆的简单性质,考查数形结合能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
18.已知数列{an}满足a1=$\frac{1}{4}$,an+1=1-$\frac{1}{a_n}$,则a2015的值为( )
| A. | $\frac{1}{4}$ | B. | -3 | C. | $\frac{2}{3}$ | D. | -2 |
5.过曲线y=xex上横坐标为1的点的切线方程为( )
| A. | 2ex-y-e=0 | B. | ex-y=0 | C. | x-y+1=0 | D. | x-y-1=0 |
15.盒中有5值LED节能灯,其中有2只是坏的,现从盒中随机地抽取2只,那么$\frac{3}{5}$是( )
| A. | 2只全是坏的概率 | B. | 2中全是好的概率 | ||
| C. | 恰有1只是坏的概率 | D. | 至少1只是坏的概率 |
20.一枚质地均匀的正四面体玩具,有三个面标有数字1,一个面标有数字2,抛掷两次,所得向上数字相同的概率是( )
| A. | $\frac{3}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | 不同于以上答案 |