题目内容
16.已知定义在R上的函数f(x)是奇函数且满足f($\frac{3}{2}$-x)=f(x),f(-2)=-3,则f(2010)+f(2012)=( )| A. | -3 | B. | -2 | C. | 3 | D. | 2 |
分析 根据函数奇偶性和对称性的性质进行转化求解即可.
解答 解:∵定义在R上的函数f(x)是奇函数且满足f($\frac{3}{2}$-x)=f(x),
∴f($\frac{3}{2}$-x)=f(x)=-f(x-$\frac{3}{2}$),
即f(x+$\frac{3}{2}$)=-f(x),
则f(x+3)=f(x+$\frac{3}{2}$+$\frac{3}{2}$)=-f(x+$\frac{3}{2}$)=f(x),
则函数的周期是3,
则f(2010)+f(2012)=f(270×3)+f(270×3+2)=f(0)+f(2)=f(2)=-f(-2)=-(-3)=3,
故选:C
点评 本题主要考查函数值的计算,根据函数奇偶性和对称性的关系求出函数的周期是解决本题的关键.

练习册系列答案
相关题目
7.已知函数f(x)由下表给出,则f(2)=3.
| x | 1 | 2 | 3 |
| f(x) | 2 | 3 | 1 |
11. 某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )
某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )
 某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )
某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )| A. | 20 | B. | 22.5 | C. | 22.75 | D. | 25 |
5.若x>0,则函数f(x)=4x+$\frac{2}{x}$的最小值是( )
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
6.将由曲线y=cosx,直线x=0,x=π,y=0所围成图形的面积写成定积分的形式为( )
| A. | ${∫}_{0}^{π}$cosxdx | B. | ${∫}_{0}^{\frac{π}{2}}$cosxdx+|${∫}_{\frac{π}{2}}^{π}$cosxdx| | ||
| C. | ${∫}_{0}^{π}$2sinxdx | D. | ${∫}_{0}^{π}$2|cosx|dx |
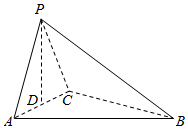 如图所示,在三棱锥P-ABC中,点P在平面ABC上的射影D与AC的中点重合,已知BC=2AC=8,AB=4$\sqrt{5}$.
如图所示,在三棱锥P-ABC中,点P在平面ABC上的射影D与AC的中点重合,已知BC=2AC=8,AB=4$\sqrt{5}$.