题目内容
已知直线l垂直平面a,垂足为O.在矩形ABCD中AD=1,AB=2,若点A在l上移动,点 B在平面a上移动,则O、D两点间的最大距离为
A.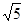 | B.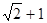 | C.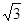 | D.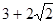 |
B
解析试题分析:因为当点点A在l上移动,点 B在平面a上移动,那么可知点B到直线L的距离为x,那么AO= ,同时有AD=1,那么结合余弦定理则有
,同时有AD=1,那么结合余弦定理则有 ,那么将数值代入表达式可知
,那么将数值代入表达式可知 ,结合根式和二次函数的性质可知O、D两点间的最大距离为
,结合根式和二次函数的性质可知O、D两点间的最大距离为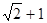 ,选B.
,选B.
考点:本试题考查了空间两点的距离的知识点。
点评:解决该试题的关键是利用线段AB的定长为2,AD为1,那么随着点A.B的运动过程中,始终保持不变的量和改变的角度OAD之间的关系式来求解OD的最大值,采用余弦定理得到分析证明,属于难度试题。

练习册系列答案
相关题目
在正方体 中,
中, ,
, 分别
分别 ,
, 是的中点,则下列判断错误的是
是的中点,则下列判断错误的是
A. 与 与 垂直 垂直 | B. 与 与 垂直 垂直 |
C. 与 与 平行 平行 | D. 与 与 平行 平行 |
已知两个不同的平面 、
、 ,能判定
,能判定 //
// 的条件是( )
的条件是( )
A. 、 、 分别平行于直线 分别平行于直线 | B. 、 、 分别垂直于直线 分别垂直于直线 |
C. 、 、 分别垂直于平面 分别垂直于平面 | D. 内有两条直线分别平行于 内有两条直线分别平行于 |
已知 为两条不同直线,
为两条不同直线, 为两个不同平面,则下列命题中不正确的是( )
为两个不同平面,则下列命题中不正确的是( )
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C.若 ,则 ,则 |
D.若 ,则 ,则 |
正方体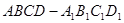 中,
中, 与平面
与平面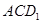 所成的角的余弦值为( )
所成的角的余弦值为( )
A.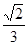 | B.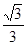 | C. | D.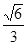 |
设 表示两条直线,
表示两条直线, 表示两个平面,则下列命题是真命题的是( )
表示两个平面,则下列命题是真命题的是( )
A.若 , , ∥ ∥ ,则 ,则 ∥ ∥ |
B.若 |
C.若 ∥ ∥ , , ,则 ,则 |
D.若 |
已知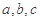 是三条不同的直线,
是三条不同的直线,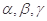 是三个不同的平面,下列命题中正确的是( )
是三个不同的平面,下列命题中正确的是( )
A.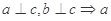 // //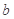 |
B.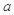 // //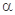 , ,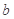 // //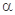 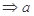 // //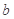 |
C.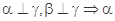 // //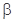 |
D.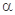 // //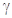 , ,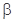 // //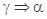 // //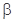 |
已知二面角 是直二面角,P为棱AB上一点,PQ、PR分别在平面
是直二面角,P为棱AB上一点,PQ、PR分别在平面 、
、 内,且
内,且 ,则
,则 为( )
为( )
| A.45° | B.60° | C.120° | D.150° |
 一边BC在平面
一边BC在平面 内,顶点A在平面
内,顶点A在平面 ,三角形所在平面与
,三角形所在平面与 ,则直线
,则直线 与
与