题目内容
10.如果实数x,y满足(x+2)2+y2=3,则$\frac{y}{x}$的最大值是$\sqrt{3}$.分析 设$\frac{y}{x}$=k,$\frac{y}{x}$的最大值就等于连接原点和圆上的点的直线中斜率的最大值,由数形结合法的方式,易得答案
解答 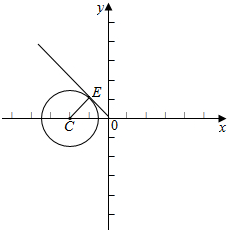 解:设$\frac{y}{x}$=k,则y=kx表示经过原点的直线,k为直线的斜率.
解:设$\frac{y}{x}$=k,则y=kx表示经过原点的直线,k为直线的斜率.
所以求$\frac{y}{x}$的最大值就等价于求同时经过原点和圆上的点的直线中斜率的最大值,
如图示:
从图中可知,斜率取最大值时对应的直线斜率为正且与圆相切,
此时的斜率就是其倾斜角∠EOC的正切值.
易得|OC|=2,|CE|=r=$\sqrt{3}$,可由勾股定理求得|OE|=1,
于是可得到k=tan∠EOC=$\frac{|CE|}{|OE|}$=$\sqrt{3}$,即为$\frac{y}{x}$的最大值.
故答案为:$\sqrt{3}$.
点评 本题考查直线与圆的位置关系,数形结合是解决问题的关键,属中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
20.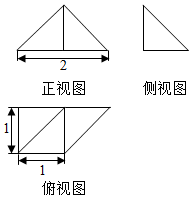 如图是一个几何体的三视图,正视图是一个等腰直角三角形,侧视图为一个直角三角形,俯视图是一个直角梯形,则此几何体的表面积是( )
如图是一个几何体的三视图,正视图是一个等腰直角三角形,侧视图为一个直角三角形,俯视图是一个直角梯形,则此几何体的表面积是( )
 如图是一个几何体的三视图,正视图是一个等腰直角三角形,侧视图为一个直角三角形,俯视图是一个直角梯形,则此几何体的表面积是( )
如图是一个几何体的三视图,正视图是一个等腰直角三角形,侧视图为一个直角三角形,俯视图是一个直角梯形,则此几何体的表面积是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{5+\sqrt{3}}{2}$ | D. | $\frac{5+\sqrt{3}}{2}$+$\sqrt{2}$ |
18.函数f(x)=lnx-x2+4x+5的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
5.已知某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 48 | B. | 4 | C. | 12 | D. | 16 |
15.若a,b是任意的实数,且a>b,则( )
| A. | |a|>|b| | B. | $\frac{b}{a}<1$ | C. | lga<lgb | D. | ${(\frac{1}{2})^a}<{(\frac{1}{2})^b}$ |
