题目内容
3.在棱长为2的正四面体ABCD中,E,F分别是BC,AD的中点,则$\overrightarrow{AE}$$•\overrightarrow{CF}$=( )| A. | 0 | B. | -2 | C. | 2 | D. | -3 |
分析 根据题意画出图形,结合图形,利用中线的性质表示出向量$\overrightarrow{AE}$与$\overrightarrow{CF}$,求出它们的数量积即可.
解答 解:如图所示,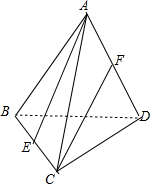
棱长为2的正四面体ABCD中,E,F分别是BC,AD的中点,
则$\overrightarrow{AE}$$•\overrightarrow{CF}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)•$\frac{1}{2}$($\overrightarrow{CA}$+$\overrightarrow{CD}$)
=$\frac{1}{4}$($\overrightarrow{AB}$•$\overrightarrow{CA}$+$\overrightarrow{AB}$•$\overrightarrow{CD}$+$\overrightarrow{AC}$•$\overrightarrow{CA}$+$\overrightarrow{AC}$•$\overrightarrow{CD}$)
=$\frac{1}{4}$(2×2×cos120°+2×2×2×cos90°+2×2×2×cos180°+2×2×cos120°)
=-3.
故选:D.
点评 本题考查了空间向量的线性表示与数量积应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.设a,b是非零实数,若a>b,则命题正确的是( )
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | a2>ab | C. | $\frac{1}{{a{b^2}}}$>$\frac{1}{{{a^2}b}}$ | D. | a2>b2 |
4.下列点不是函数f(x)=tan(2x+$\frac{π}{3}$)的图象的一个对称中心的是( )
| A. | (-$\frac{2π}{3}$,0) | B. | ($\frac{2π}{3}$,0) | C. | ($\frac{π}{12}$,0) | D. | (-$\frac{π}{6}$,0) |
8.已知向量$\overrightarrow a$=(cos($\frac{π}{2}$-x),sin($\frac{π}{2}$+x)),$\overrightarrow b$=(sin($\frac{π}{2}$+x),sinx),若x=-$\frac{π}{12}$,则向量$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |