题目内容
某产品的广告费用x万元与销售额y万元的统计数据如下表:
根据上表可得回归方程
=9x+10.5,则m为( )
| 广告费用x(万元) | 4 | 2 | 3 | 5 |
| 销售额y(万元) | 49 | 26 | 39 | m |
 |
| y |
| A、54 | B、53 | C、52 | D、51 |
考点:回归分析
专题:计算题,概率与统计
分析:根据线性回归直线过样本中心点,即可求出m的值.
解答:
解:由题意,
=
(4+2+3+5)=3.5,代入
=9x+10.5,可得
=42,
∴
(49+26+39+m)=42,得m=54.
故选A.
. |
| x |
| 1 |
| 4 |
 |
| y |
. |
| y |
∴
| 1 |
| 4 |
故选A.
点评:本题考查线性回归方程的求法和应用,是一个基础题,本题解答关键是利用线性回归直线必定经过样本中心点.

练习册系列答案
相关题目
椭圆C:
+
=1的左、右顶点分别为A1,A2,点P在C上且直线PA2的斜率的取值范围是[-3,-1],那么直线PA1斜率的取值范围是( )
| x2 |
| 4 |
| y2 |
| 3 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
tan300°+
的值是( )
| cos(-4050) |
| sin7650 |
A、1+
| ||
B、1-
| ||
C、-1-
| ||
D、-1+
|
已知m,n为不同的直线,α,β为不同的平面,则下列说法正确的是( )
| A、m?α,n∥m⇒n∥α |
| B、m?α,n⊥m⇒n⊥α |
| C、m?α,n?β,m∥n⇒α∥β |
| D、n?β,n⊥α⇒α⊥β |
已知条件p:x>1或x<-3,条件q:x>a,且q是p的充分而不必要条件,则a的取值范围是( )
| A、a≥1 | B、a≤1 |
| C、a≥-3 | D、a≤-3 |
执行如图所示的程序框图,如果输入的N值是6,那么输出p的值是( )

| A、15 | B、105 |
| C、120 | D、720 |
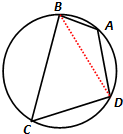 已知圆内接四边形ABCD的边AB=1,BC=3,CD=DA=2.
已知圆内接四边形ABCD的边AB=1,BC=3,CD=DA=2.