题目内容
8.已知直线l:(m+2)x+(m-1)y+4-4m=0上总存在点M,使得过M点作的圆C:x2+y2+2x-4y+3=0的两条切线互相垂直,则实数m的取值范围是( )| A. | m≤1或m≥2 | B. | 2≤m≤8 | C. | -2≤m≤10 | D. | m≤-2或m≥8 |
分析 若直线l上总存在点M使得过点M的两条切线互相垂直,只需圆心(-1,2)到直线l的距离$d=\frac{|-m-2+2m-2+4-4m|}{{\sqrt{{{(m+2)}^2}+{{(m-1)}^2}}}}≤2$,即可求出实数m的取值范围.
解答 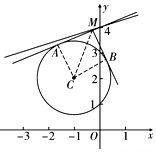 解:如图,设切点分别为A,B.连接AC,BC,MC,
解:如图,设切点分别为A,B.连接AC,BC,MC,
由∠AMB=∠MAC=∠MBC=90°及MA=MB知,四边形MACB为正方形,故$|MC|=\sqrt{2+2}=2$,
若直线l上总存在点M使得过点M的两条切线互相垂直,只需圆心(-1,2)到直线l的距离$d=\frac{|-m-2+2m-2+4-4m|}{{\sqrt{{{(m+2)}^2}+{{(m-1)}^2}}}}≤2$,即m2-8m-20≤0,∴-2≤m≤10,
故选:C.
点评 本题考查直线和圆的位置关系,由题意得到若直线l上总存在点M使得过点M的两条切线互相垂直,只需圆心(-1,2)到直线l的距离$d=\frac{|-m-2+2m-2+4-4m|}{{\sqrt{{{(m+2)}^2}+{{(m-1)}^2}}}}≤2$,是解决问题的关键,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.从狼堡去青青草原的道路有6条,从青青草原去羊村的道路有20条,狼堡与羊村被青青草原隔开,则狼去羊村的不同走法有( )
| A. | 120 | B. | 26 | C. | 20 | D. | 6 |
3.若点P(x,y)在线段AB上运动,且A(4,0),B(0,2),设T=log2x+log2y,则( )
| A. | T有最大值2 | B. | T有最小值1 | ||
| C. | T有最大值1 | D. | T没有最大值和最小值 |
20.下列函数中不是奇函数的是( )
| A. | $y=\frac{{({{a^x}+1})x}}{{{a^x}-1}}({a>0,a≠1})$ | B. | $y=\frac{{{a^x}-{a^{-x}}}}{2}({a>0,a≠1})$ | ||
| C. | $y=\left\{\begin{array}{l}1,({x>0})\\-1,({x<0})\end{array}\right.$ | D. | $y={log_a}\frac{1+x}{1-x}({a>0,a≠1})$ |