题目内容
已知正项数列{an}中,对于一切的n∈N*均有a ≤an-an+1成立.
≤an-an+1成立.
(1)证明:数列{an}中的任意一项都小于1;
(2)探究an与 的大小,并证明你的结论.
的大小,并证明你的结论.
(1)由a ≤an-an+1得an+1≤an-a
≤an-an+1得an+1≤an-a .
.
∵在数列{an}中an>0,∴an+1>0,
∴an-a >0,∴0<an<1,
>0,∴0<an<1,
故数列{an}中的任何一项都小于1.
(2)解法1:由(1)知0<an<1= ,
,
那么a2≤a1-a =-
=-
由此猜想:an< .
.
下面用数学归纳法证明:当n≥2,n∈N时猜想正确.
①当n=2时,显然成立;
②假设当n=k(k≥2,k∈N)时,有ak< ≤
≤ 成立.
成立.
那么ak+1≤ak-a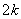 =-
=-
∴当n=k+1时,猜想也正确.
综上所述,对于一切n∈N*,都有an< .
.
解法2:由a ≤an-an+1,
≤an-an+1,
得0<ak+1≤ak-a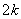 =ak(1-ak),
=ak(1-ak),
 令k=1,2,3,…,n-1得:
令k=1,2,3,…,n-1得:


练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
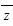 1=
1=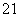 =z
=z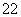
 +a
+a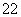 =1,则a1+a2≤
=1,则a1+a2≤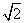 ”的证明过程:证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以Δ≤0,从而得4(a1+a2)2-8≤0,所以a1+a2≤
”的证明过程:证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以Δ≤0,从而得4(a1+a2)2-8≤0,所以a1+a2≤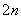 =1时,你能得到的结论为____________________(不必证明).
=1时,你能得到的结论为____________________(不必证明). (n∈N*)的第二步中,当n=k+1时等式左边与n=k时等式左边的差等于________.
(n∈N*)的第二步中,当n=k+1时等式左边与n=k时等式左边的差等于________.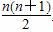 .
.

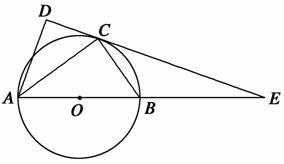
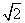 ,求BC的长.
,求BC的长.