题目内容
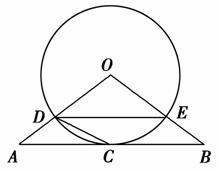
如图，在△ABC和△ACD中，∠ACB＝∠ADC＝90°，∠BAC＝∠CAD，⊙O是以AB为直径的圆，DC的延长线与AB的延长线交于点E.
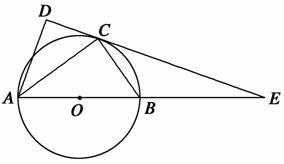
(1)求证：DC是⊙O的切线；
(2)若EB＝6，EC＝6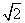
，求BC的长．
(1)∵AB是⊙O的直径，∠ACB＝90°，
∴点C在⊙O上，
连接OC，可得∠OCA＝∠OAC＝∠DAC，∴OC∥AD，
又∵AD⊥DC，∴DC⊥OC，
∵OC为半径，
∴DC是⊙O的切线．
(2)∵DC是⊙O的切线，
∴EC2＝EB·EA.
又∵EB＝6，EC＝6，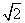
∴EA＝12，AB＝6.
∵∠ECB＝∠EAC，∠CEB＝∠AEC，
∴△ECB
△EAC，
∴
＝
＝
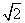，∴AC＝BC.
∵AC2＋BC2＝AB2＝36，∴BC＝2
.
练习册系列答案
相关题目
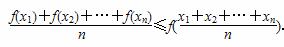．若y＝sinx在区间(0，π)上是凸函数，那么在△ABC中，sinA＋sinB＋sinC的最大值是________．
≤an－an＋1成立．
的大小，并证明你的结论．
的值为________．
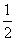，求⊙O的半径r的长．
(t为参数)，则直线的倾斜角为( )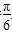
.