题目内容
【题目】已知双曲线
的左,右焦点分别为
,若双曲线上存在点
,使
,则该双曲线的离心率
范围为（ ）
A. （1,1
） B. （1,1
） C. （1,1
] D. （1,1
]
【答案】A
【解析】由题意，点
不是双曲线的顶点，否则
无意义，在
中，由正弦定理得
，又
，即
， 
在双曲线的右支上，由双曲线的定义，得
，即
，由双曲线的几何性质，知
，即
， 
，解得
，又
，所以双曲线离心率的范围是
，故选A.
【方法点晴】本题主要考查正弦定理以及利用双曲线的简单性质求双曲线的离心率范围，属于难题.求解与双曲线性质有关的问题时要结合图形进行分析，既使不画出图形，思考时也要联想到图形，当涉及顶点、焦点、实轴、虚轴、渐近线等双曲线的基本量时，要理清它们之间的关系，挖掘出它们之间的内在联系.求离心率问题应先将 
用有关的一些量表示出来，再利用其中的一些关系构造出关于
的不等式，从而求出
的范围.焦半径构造出关于
的不等式，最后解出
的范围.
练习册系列答案
相关题目
【题目】交管部门为宣传新交规举办交通知识问答活动，随机对该市
岁的人群抽样了
人，回答问题统计结果如图表所示：
分组 | 回答正确的人数 | 回答正确的人数占本组的频率 | |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
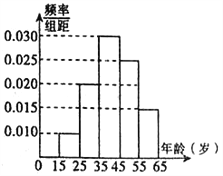
（1）分别求出
，
，
，
的值；
（2）从第
，
，
组回答正确的人中用分层抽样方法抽取
人，则第，，组每组应各抽取多少人？
（3）在（2）的前提下，决定在所抽取的人中随机抽取人颁发幸运奖，求：所抽取的人中至少有一个第组的人的概率.
