题目内容
【题目】以原点
为极点，
轴的非负半轴为极轴建立极坐标系，已知曲线
的极坐标方程为：
，在平面直角坐标系
中，直线
的方程为
（
为参数）．
（1）求曲线和直线的直角坐标方程；
（2）已知直线交曲线于
，
两点，求，两点的距离．
【答案】(1)曲线
化为普通方程为
，直线
的直角坐标方程为
．(2)
.
【解析】【试题分析】（1）对曲线的极坐标方程两边乘以
,即可得到直角坐标方程.利用加减消元法消掉参数,可得到直线的直角坐标方程.(2)将直线的参数方程代入圆的方程中,利用参数的几何意义可求得两点距离.
【试题解析】
（1）由题知，曲线化为普通方程为
，
直线的直角坐标方程为
．
（2）由题知，直线的参数方程为
（
为参数），
代入曲线：中，化简，得
，
设
，
两点所对应的参数分别为
，
，则
所以
，即，的距离为．
【题目】某百货商店今年春节期间举行促销活动，规定消费达到一定标准的顾客可进行一次抽奖活动，随着抽奖活动的有效开展，参与抽奖活动的人数越来越多，该商店经理对春节前
天参加抽奖活动的人数进行统计，
表示第
天参加抽奖活动的人数，得到统计表格如下：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 8 | 8 | 10 | 14 | 15 | 17 |
（Ⅰ）经过进一步统计分析，发现与具有线性相关关系.请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
（Ⅱ）该商店规定：若抽中“一等奖”，可领取
元购物券；抽中“二等奖”可领取
元购物券；抽中“谢谢惠顾”，则没有购物券.已知一次抽奖活动获得“一等奖”的概率为
，获得“二等”的概率为
.现有张、王两位先生参与了本次活动，且他们是否中奖相互独立，求此二人所获购物券总金额
的分布列及数学期望.
参考公式：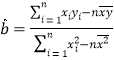
，
，
.
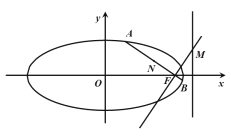
【题目】【2018山西太原市高三3月模拟】已知椭圆
的左、右顶点分别为
，右焦点为
，点
在椭圆
上．
（I）求椭圆方程；
（II）若直线
与椭圆
交于
两点，已知直线
与
相交于点
，证明：点
在定直线上，并求出定直线的方程．
【题目】从某工厂的一个车间抽取某种产品50件，产品尺寸（单位：
）落在各个小组的频数分布如下表：
数据分组 |
|
|
|
|
|
|
|
频数 | 3 | 8 | 9 | 12 | 10 | 5 | 3 |
（1）根据频数分布表，求该产品尺寸落在
的概率；
（2）求这50件产品尺寸的样本平均数
.（同一组中的数据用该组区间的中点值作代表）；
（3）根据产品的频数分布，求出产品尺寸中位数的估计值.
