题目内容
16.在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的上下顶点分别为A,B,右顶点为C,右焦点为F,延长BF与AC交于点P,若O,F,P,A四点共圆,则该椭圆的离心率为( )| A. | $\frac{{\sqrt{2}-1}}{2}$ | B. | $\frac{{\sqrt{3}-1}}{2}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{\sqrt{5}-\sqrt{2}}}{2}$ |
分析 由O,F,P,A四点共圆得$∠APF=\frac{π}{2}$,即AC⊥BP,∴${k_{AC}}•{k_{BP}}=-\frac{b}{a}•\frac{b}{c}=-1$,b2=ac,e2+e-1=0
解答 解:如图所示,∵O,F,P,A四点共圆,$∠AOF=\frac{π}{2}$,∴$∠APF=\frac{π}{2}$,
即AC⊥BP,∴${k_{AC}}•{k_{BP}}=-\frac{b}{a}•\frac{b}{c}=-1$,
∴b2=ac,a2-c2=ac,∴e2+e-1=0,$e=\frac{{\sqrt{5}-1}}{2}$,
故选C.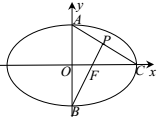
点评 本题考查了椭圆的离心率,运用平面几何知识及椭圆定义是解题关键,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
6.已知$a=\frac{2}{5}$,$b={2^{\frac{1}{2}}}$,$c=log_3^{\frac{1}{2}}$,则( )
| A. | b>c>a | B. | c>b>a | C. | b>a>c | D. | a>b>c |
7.在一次比赛中某队共有甲,乙,丙等5位选手参加,赛前用抽签的方法决定出场的顺序,则乙、丙都不与甲相邻出场的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{10}$ |
8.已知集合M={x|x2-2x-3≤0},N={x|log2x>1},则M∩N=( )
| A. | [-1,2) | B. | [-1,+∞) | C. | (2,3] | D. | (2,+∞) |
6.已知集合A={x|x2-3x-10<0,x∈N*},B={2x<16},则A∩B=( )
| A. | {-1,0,1,2,3} | B. | {1,2,3,4} | C. | {1,2,3} | D. | {1} |