已知集合M={x|x2-2x-3≤0}.N={x|log2x＞1}.则M∩N=( )A．[-1.2)B．[-1.+∞)C．(2.3]D．题目和参考答案——青夏教育精英家教网—

题目内容

8．已知集合M={x|x²-2x-3≤0}，N={x|log₂x＞1}，则M∩N=（　　）

A．

[-1，2）

B．

[-1，+∞）

C．

（2，3]

D．

（2，+∞）

分析求出M与N中不等式的解集确定出M与N，找出两集合的交集即可．

解答解：∵x²-2x-3≤0，
∴（x-3）（x+1）≤0，
解得-1≤x≤3，
∴M=[-1，3]，
由N中log₂x＞1=log₂2，得到x＞2，即M=（2，+∞），
则M∩N=（2，3]．
故选：C．

点评此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

19．一个几何体的三视图如图所示，则其体积为（　　）

16．在平面直角坐标系xOy中，已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的上下顶点分别为A，B，右顶点为C，右焦点为F，延长BF与AC交于点P，若O，F，P，A四点共圆，则该椭圆的离心率为（　　）

A．

$\frac{{\sqrt{2}-1}}{2}$

B．

$\frac{{\sqrt{3}-1}}{2}$

C．

$\frac{{\sqrt{5}-1}}{2}$

D．

$\frac{{\sqrt{5}-\sqrt{2}}}{2}$

3．设函数f（x）=e^2x，g（x）=kx+1（k∈R）．
（Ⅰ）若直线y=g（x）和函数y=f（x）的图象相切，求k的值；
（Ⅱ）当k＞0时，若存在正实数m，使对任意x∈（0，m），都有|f（x）-g（x）|＞2x恒成立，求k的取值范围．

13．

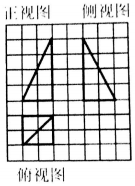如图所示，网格纸上小正方形的边长为1，粗线画出的是某一几何体的三视图，则该几何体外接球的表面积为（　　）

20．已知函数f（x）=e^x，g（x）=kx+1，且直线y=g（x）和函数y=f（x）的图象相切．
（Ⅰ）求实数k的值；
（Ⅱ）设h（x）=f（x）-g（x），若不等式（m-x）h′（x）＜x+1对任意x∈（0，+∞）恒成立（m∈Z，h′（x）为h（x）的导函数），求m的最大值..

17．（$\sqrt{x}$-2x）⁵的展开式中，含x³项的系数是（　　）

18．已知函数f（x）=ln（x-1）+$\frac{ax}{x+1}$（a∈R）．
（1）若函数f（x）在区间（1，4）上单调递增，求a的取值范围；
（2）若函数y=f（x）的图象与直线4x-3y-2=0相切，求a的值．

试题分类