题目内容
 函数f(x)=2sin(ωx+φ)
函数f(x)=2sin(ωx+φ)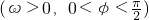 的部分图象如下图所示,该图象与y轴交于点F(0,1),与x轴交于点B,C,M为最高点,且三角形MBC的面积为π.
的部分图象如下图所示,该图象与y轴交于点F(0,1),与x轴交于点B,C,M为最高点,且三角形MBC的面积为π.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若 ,求
,求 的值.
的值.
解:(I)∵ ,∴周期
,∴周期 .
.
由f(0)=2sinφ=1,得 ,又∵
,又∵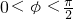 ,∴
,∴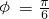 ,
,
∴ .
.
(Ⅱ)由 ,得
,得 .
.
∵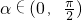 ,∴
,∴ ,
,
∴ ,
,
∴ =
= .
.
分析:(I)根据三角形MBC的面积为π求得BC的值,可得函数的周期,从而求得ω的值,再把点(0,1)代入求得φ的值,从而得到函数的解析式.
(Ⅱ)由 ,得
,得 ,再利用同角三角函数的基本关系求得cosα的值,利用二倍角公式、两角和差的余弦公式求得
,再利用同角三角函数的基本关系求得cosα的值,利用二倍角公式、两角和差的余弦公式求得 的值.
的值.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,同角三角函数的基本关系以及二倍角公式的应用,属于中档题.
 ,∴周期
,∴周期 .
.由f(0)=2sinφ=1,得
 ,又∵
,又∵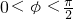 ,∴
,∴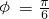 ,
,∴
 .
.(Ⅱ)由
 ,得
,得 .
.∵
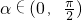 ,∴
,∴ ,
,∴
 ,
,∴
 =
= .
.分析:(I)根据三角形MBC的面积为π求得BC的值,可得函数的周期,从而求得ω的值,再把点(0,1)代入求得φ的值,从而得到函数的解析式.
(Ⅱ)由
 ,得
,得 ,再利用同角三角函数的基本关系求得cosα的值,利用二倍角公式、两角和差的余弦公式求得
,再利用同角三角函数的基本关系求得cosα的值,利用二倍角公式、两角和差的余弦公式求得 的值.
的值.点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,同角三角函数的基本关系以及二倍角公式的应用,属于中档题.

练习册系列答案
相关题目