题目内容
((本小题满分12分)
如图,已知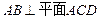 ,
,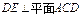 ,
,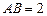 ,
,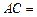
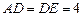 ,
,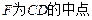 .
.
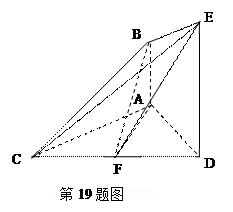
(Ⅰ)求证: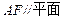
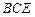 ;
;
(Ⅱ) 若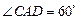 ,求二面角
,求二面角 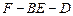 的余弦值.
的余弦值.
如图,已知
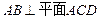 ,
,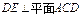 ,
,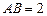 ,
,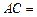
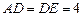 ,
,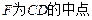 .
.
(Ⅰ)求证:
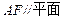
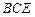 ;
; (Ⅱ) 若
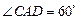 ,求二面角
,求二面角 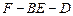 的余弦值.
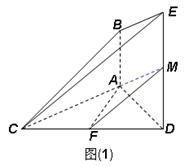
的余弦值.证法一(Ⅰ):如图(1),取 的中点M,连接AM,FM,
的中点M,连接AM,FM,
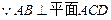 ,
, ∴
∴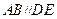 .
.
 ,
,
∴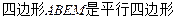 ,∴AM∥BE
,∴AM∥BE
又∵ ,
,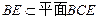 ,
,
∴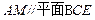 .
.
∵CF="FD,DM=ME, " ∴MF∥CE,
 又∵
又∵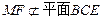 ,
, ,
,
∴ , 又∵
, 又∵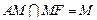 ,
,
∴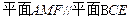 ,
,
∵ ,
,
∴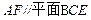 .-------5分
.-------5分
证法二:如图(2),取CE的中点N,连接FN,BN,
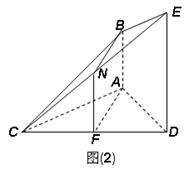
∵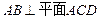 ,
,
∴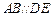 ,
,
∵CF=FD,CN="NE, " ∴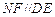 ,
, ,
,
又 , ∴
, ∴ ,
, ,
,
∴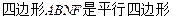 ,
,
∴AF∥BN, 又∵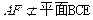 ,
, ,
,
∴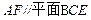 .------5分
.------5分
(Ⅱ)解法一:如图(3)过F作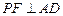 交AD于点P,作PG⊥BE,连接FG.
交AD于点P,作PG⊥BE,连接FG.

∵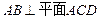 ,
, ,
,
∴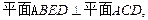
∴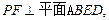 ∴FG⊥BE(三垂线定理).
∴FG⊥BE(三垂线定理).
所以,∠PGF就是二面角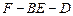 的平面角.
的平面角.
由 ,
,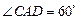 ,知△
,知△ 是正三角形,
是正三角形,
在Rt△DPF中,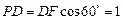 ,
,  ,∴PA=3,
,∴PA=3,
∴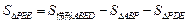
 ,
,
∵ , ∴
, ∴
∴在Rt△PGF中,由勾股定理,得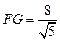 ,
,
∴ ,即二面角
,即二面角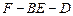 的余弦值为
的余弦值为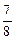 .----12分
.----12分
解法二:以A为原点,分别以AC,AB为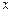 轴、
轴、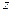 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系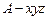 ,
,
如图(4)所示,则A(0,0,0),B(0,0,2),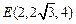 ,
, ,于是,有
,于是,有

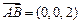 ,
,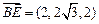 ,
,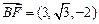 ,
,
设平面BEF的一个法向量为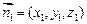 ,则
,则
 令
令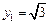 ,可得,
,可得,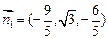
设平面ABED的一个法向量为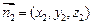 ,则
,则

 ,可得,
,可得,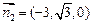
∴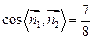
所以,所求的二面角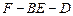 的余弦值为
的余弦值为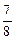 .------12分
.------12分
 的中点M,连接AM,FM,
的中点M,连接AM,FM,
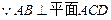 ,
, ∴
∴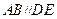 .
. ,
,∴
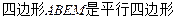 ,∴AM∥BE
,∴AM∥BE又∵
 ,
,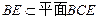 ,
,∴
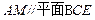 .
.∵CF="FD,DM=ME, " ∴MF∥CE,
 又∵
又∵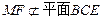 ,
, ,
,∴
 , 又∵
, 又∵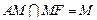 ,
,∴
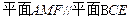 ,
, ∵
 ,
,∴
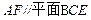 .-------5分
.-------5分证法二:如图(2),取CE的中点N,连接FN,BN,

∵
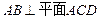 ,
,
∴
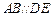 ,
,∵CF=FD,CN="NE, " ∴
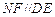 ,
, ,
,又
 , ∴
, ∴ ,
, ,
,∴
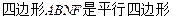 ,
,∴AF∥BN, 又∵
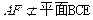 ,
, ,
,∴
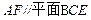 .------5分
.------5分(Ⅱ)解法一:如图(3)过F作
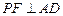 交AD于点P,作PG⊥BE,连接FG.
交AD于点P,作PG⊥BE,连接FG.
∵
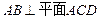 ,
, ,
,∴
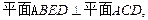
∴
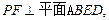 ∴FG⊥BE(三垂线定理).
∴FG⊥BE(三垂线定理).所以,∠PGF就是二面角
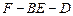 的平面角.
的平面角.由
 ,
,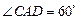 ,知△
,知△ 是正三角形,
是正三角形,在Rt△DPF中,
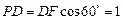 ,
,  ,∴PA=3,
,∴PA=3,∴
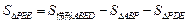
 ,
,∵
 , ∴
, ∴
∴在Rt△PGF中,由勾股定理,得
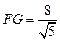 ,
,∴
 ,即二面角
,即二面角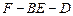 的余弦值为
的余弦值为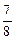 .----12分
.----12分解法二:以A为原点,分别以AC,AB为
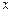 轴、
轴、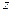 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系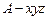 ,
,如图(4)所示,则A(0,0,0),B(0,0,2),
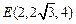 ,
, ,于是,有
,于是,有
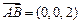 ,
,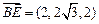 ,
,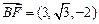 ,
,设平面BEF的一个法向量为
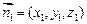 ,则
,则 令
令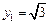 ,可得,
,可得,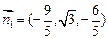
设平面ABED的一个法向量为
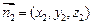 ,则
,则
 ,可得,
,可得,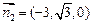
∴
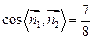
所以,所求的二面角
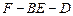 的余弦值为
的余弦值为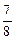 .------12分
.------12分略

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
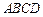 是圆柱
是圆柱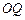 的轴截面,点
的轴截面,点 在圆柱
在圆柱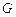 是
是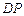 的中点,圆柱
的中点,圆柱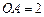 ,侧面积为
,侧面积为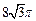 ,
,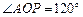 .
.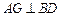 ;
;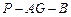 的平面角的余弦值.
的平面角的余弦值.
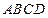 为直角梯形,
为直角梯形,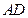 //
//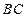 ,
,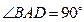 ,
, 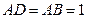 ,
, 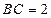 ,
, 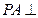 平面
平面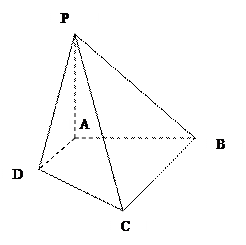
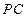 与
与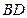 所成的角为
所成的角为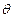 ,且
,且 ,求
,求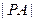 ;
;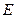 为
为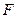 ,使
,使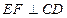 ?
?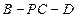 的大小.
的大小.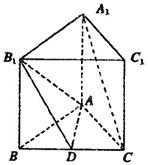
 3)求点C到平面AB1D的距离.
3)求点C到平面AB1D的距离.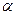 上有一长方体
上有一长方体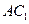 绕
绕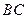 旋转
旋转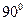 得到如图所示的几何体.
得到如图所示的几何体.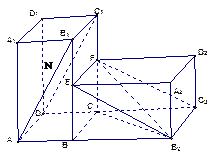
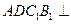 平面
平面 ;
;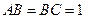 时,直线
时,直线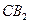 与平面
与平面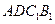 所成的角的正弦值为
所成的角的正弦值为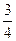 ,求
,求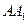 的长度;
的长度;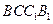 与平面
与平面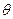 ,
, 长方体
长方体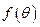 ,请直接写出
,请直接写出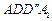 和
和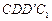 都是正方形。将两个正方形分别沿AD,CD折
都是正方形。将两个正方形分别沿AD,CD折 起,使
起,使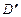 与
与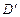 重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面A
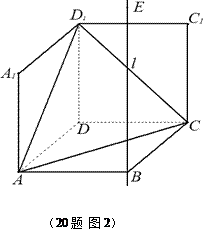
重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面A BCD同侧,设
BCD同侧,设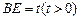 (图2)。
(图2)。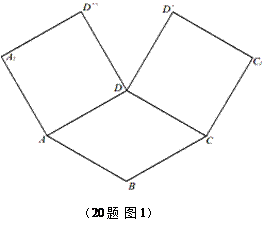
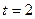 时,求
时,求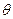 的余弦值;
的余弦值;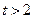 时在线段
时在线段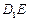 上是否存在点
上是否存在点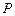 ,使平面
,使平面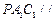 平面
平面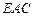 ,若存在,求出
,若存在,求出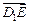 所成的比
所成的比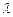 ;若不存在,请说明理由。
;若不存在,请说明理由。
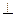 底面BCD,若
底面BCD,若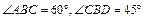 ,则侧棱AB与底面BCD所 成的角为 .
,则侧棱AB与底面BCD所 成的角为 .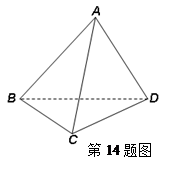
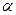 相交的线段
相交的线段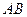 ,其长度为10cm,两端点
,其长度为10cm,两端点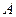 、
、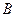 到平面
到平面 面a所成的角是 .
面a所成的角是 .