题目内容
(本小题满分13分)
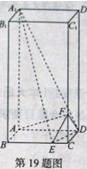
已知,在水平平面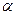 上有一长方体
上有一长方体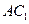 绕
绕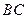 旋转
旋转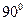 得到如图所示的几何体.
得到如图所示的几何体.
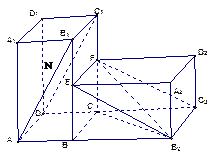
(Ⅰ)证明:平面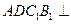 平面
平面 ;
;
(Ⅱ)当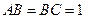 时,直线
时,直线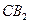 与平面
与平面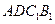 所成的角的正弦值为
所成的角的正弦值为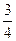 ,求
,求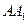 的长度;
的长度;
(Ⅲ)在(Ⅱ)条件下,设旋转过程中,平面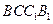 与平面
与平面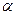 所成的角为
所成的角为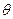 ,
, 长方体
长方体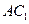 的最高点离平面
的最高点离平面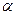 的距离为
的距离为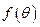 ,请直接写出
,请直接写出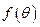 的一个表达式,并注明定义域.
的一个表达式,并注明定义域.
已知,在水平平面
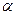 上有一长方体
上有一长方体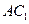 绕
绕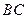 旋转
旋转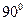 得到如图所示的几何体.
得到如图所示的几何体.
(Ⅰ)证明:平面
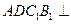 平面
平面 ;
;(Ⅱ)当
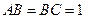 时,直线
时,直线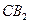 与平面
与平面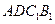 所成的角的正弦值为
所成的角的正弦值为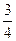 ,求
,求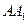 的长度;
的长度;(Ⅲ)在(Ⅱ)条件下,设旋转过程中,平面
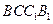 与平面
与平面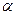 所成的角为
所成的角为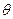 ,
, 长方体
长方体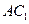 的最高点离平面
的最高点离平面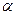 的距离为
的距离为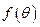 ,请直接写出
,请直接写出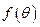 的一个表达式,并注明定义域.
的一个表达式,并注明定义域.证明:(Ⅰ)延长 交
交 于
于 ,
,  ,
,
 ,
,
 ,
,
 ,
,

即 ……………………………………2分
……………………………………2分
又
 ……………………………………3分
……………………………………3分
 , ……………………………………4分
, ……………………………………4分

 平面
平面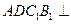 平面
平面 ;……………………………………5分
;……………………………………5分
(Ⅱ)如图,以 所在直线为x轴,y轴,z轴,建立空间直角坐标系
所在直线为x轴,y轴,z轴,建立空间直角坐标系 ,
,
设 ……………………………………6分
……………………………………6分

 ……………………………………7分
……………………………………7分
设平面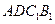 的一个法向量为
的一个法向量为 ,
,
则由 ,取
,取 ……………………………………8分
……………………………………8分
设直线
解得 ……………………………………10分
……………………………………10分
(Ⅲ) ……………………………………13分
……………………………………13分
 交
交 于
于 ,
,  ,
, ,
, ,
, ,
,
即
 ……………………………………2分
……………………………………2分又

 ……………………………………3分
……………………………………3分 , ……………………………………4分
, ……………………………………4分
 平面
平面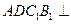 平面
平面 ;……………………………………5分
;……………………………………5分(Ⅱ)如图,以
 所在直线为x轴,y轴,z轴,建立空间直角坐标系
所在直线为x轴,y轴,z轴,建立空间直角坐标系 ,
,设
 ……………………………………6分
……………………………………6分
 ……………………………………7分
……………………………………7分设平面
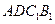 的一个法向量为
的一个法向量为 ,
,则由
 ,取
,取 ……………………………………8分
……………………………………8分设直线

解得
 ……………………………………10分
……………………………………10分(Ⅲ)
 ……………………………………13分
……………………………………13分略

练习册系列答案
相关题目
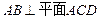 ,
,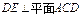 ,
,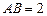 ,
,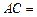
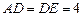 ,
,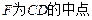 .
.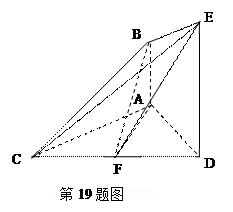
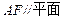
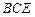 ;
; 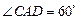 ,求二面角
,求二面角 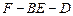 的余弦值.
的余弦值.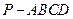 中,底面ABCD为矩形,
中,底面ABCD为矩形,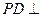 底面ABCD,AD=PD=1,AB=
底面ABCD,AD=PD=1,AB=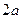 (
(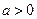 ),E,F分别CD.PB的中点。
),E,F分别CD.PB的中点。
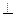 平面PAB;,
平面PAB;,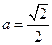 时,求AC与平面AEF所成角的正弦值。
时,求AC与平面AEF所成角的正弦值。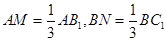 ,则下列结论①
,则下列结论①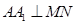 ;②
;②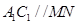 ;③MN//平面A1B1C1D1;④
;③MN//平面A1B1C1D1;④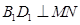 中,正确命题的个数是 ( )
中,正确命题的个数是 ( )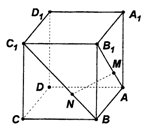
 -ABC的底面是边长为2的正三角形,顶点
-ABC的底面是边长为2的正三角形,顶点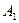 在底面上的射影是△ABC的中心,
在底面上的射影是△ABC的中心, 与AB的夹角是45°
与AB的夹角是45°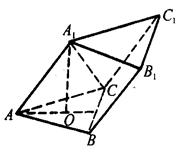
 1)求证:
1)求证: ⊥平面
⊥平面 ;
;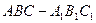 的所有棱长都为4,
的所有棱长都为4, 为
为 的中点.
的中点.
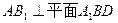 ;
;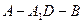 的大小.
的大小. 的外接球球心在
的外接球球心在 上,且
上,且 ,
, ,在外接球面上
,在外接球面上 两点
两点 间的球面距离是 。
间的球面距离是 。 12分)
12分)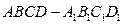 中,
中,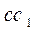 上的点,CF=AB=2CE,
上的点,CF=AB=2CE,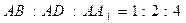 .
.
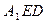 ;
;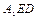 与平面FED
与平面FED 所成的角的余弦值.
所成的角的余弦值.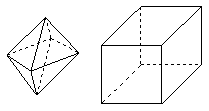
 3个
3个