题目内容
9.将cos2x+sin2x化为Asin(x+θ)的形式,若函数f(x)=Asin(x+θ),则其值域为[-$\sqrt{2}$$\sqrt{2}$].分析 利用两角和差的正弦公式化简函数的解析式,再利用正弦函数的值域,得出结论.
解答 解:cos2x+sin2x=$\sqrt{2}$($\frac{\sqrt{2}}{2}$cos2x+$\frac{\sqrt{2}}{2}$sin2x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$)∈[-$\sqrt{2}$ $\sqrt{2}$],
故答案为:[-$\sqrt{2}$ $\sqrt{2}$].
点评 本题主要考查两角和差的正弦公式,正弦函数的值域,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列三角函数值大小比较正确的是( )
| A. | sin$\frac{19π}{8}$<cos$\frac{14π}{9}$ | B. | sin(-$\frac{54π}{7}$)<sin(-$\frac{63π}{8}$) | ||
| C. | tan(-$\frac{13π}{4}$)>tan(-$\frac{17π}{5}$) | D. | tan138°>tan143° |
17.双曲线$\frac{y^2}{9}-\frac{x^2}{4}=1$的渐近线方程为( )
| A. | $y=±\frac{9}{4}x$ | B. | $y=±\frac{4}{9}x$ | C. | $y=±\frac{2}{3}x$ | D. | $y=±\frac{3}{2}x$ |
4.已知点A(2,1)和B(-1,3),若直线3x-2y-a=0与线段AB相交,则a的取值范围是( )
| A. | -4≤a≤9 | B. | a≤-4或a≥9 | C. | -9≤a≤4 | D. | a≤-9或a≥4 |
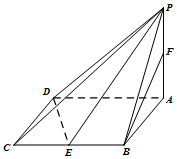 在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA⊥面ABCD,PA=$\sqrt{3}$,E,F分别为BC,PA的中点.
在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA⊥面ABCD,PA=$\sqrt{3}$,E,F分别为BC,PA的中点.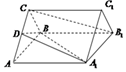 如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.
如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.