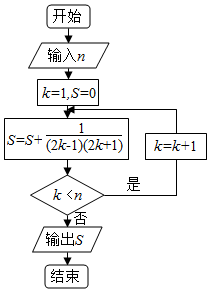
题目内容
4.随机变量a服从正态分布N(1,σ2),且P(0<a<1)=0.3000.已知a>0,a≠1,则函数y=ax+1-a图象不经过第二象限的概率为( )| A. | 0.3750 | B. | 0.3000 | C. | 0.2500 | D. | 0.2000 |
分析 随机变量ξ服从正态分布N(1,σ2),得到曲线关于x=1对称,根据曲线的对称性得到大于2的数据的概率,根据概率的性质得到结果.
解答 解:∵y=ax+1-a图象不经过第二象限,
∴1-a≤-1,
∴a≥2,
随机变量ξ服从正态分布N(1,σ2),且P(0<a<1)=0.3000,
∴P(1<a<2)=0.3000,
∴P(a>2)=0.2000,
∴函数y=ax+1-a图象不经过第二象限的概率为$\frac{0.2}{1-0.2}$=0.2500,
故选:C
点评 本题考查正态分布曲线的特点及曲线所表示的意义,考查概率的性质,是一个基础题.

练习册系列答案
相关题目
13.已知集合M={x|x<0},N={x|x2-x-2<0},则M∩N=( )
| A. | {x|-1<x<0} | B. | {x|-2<x<0} | C. | {x|x<2} | D. | {x|x<1} |
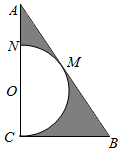 如图所示,△ABC中,∠C=90°,∠B=60°,AB=2$\sqrt{3}$,在三角形内挖去半圆(圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于N),则图中阴影部分绕直线AC旋转一周所得旋转体的内外表面积之比为$\frac{4}{9}$.
如图所示,△ABC中,∠C=90°,∠B=60°,AB=2$\sqrt{3}$,在三角形内挖去半圆(圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于N),则图中阴影部分绕直线AC旋转一周所得旋转体的内外表面积之比为$\frac{4}{9}$.