题目内容
11.设等比数列{an}的前n项和为Sn,若S10:S5=1:2,则S15:S5=3:4.分析 本题可由等比数列的性质,每连续五项的和是一个等比数列求解,由题设中的条件S10:S5=1:2,可得出(S10-S5):S5=-1:2,由此得每连续五项的和相等,由此规律易得所求的比值.
解答 解:∵等比数列{an}的前n项和为Sn,若S10:S5=1:2,
∴(S10-S5):S5=-1:2,
由等比数列的性质得(S15-S10):(S10-S5):S5=1:(-2):4,
∴S15:S5=3:4,
故答案为:3:4.
点评 本题考查等比数列的性质,解题的关键是熟练掌握等比数列的性质,是基础题.

练习册系列答案
相关题目
18. 某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
(1)请在图中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.
相关公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{1}}^{2}-n\overline{{x}^{2}}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
 某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.
相关公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{1}}^{2}-n\overline{{x}^{2}}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
 为等比数列
为等比数列 的前
的前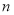 项和,
项和,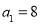 ,且
,且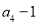 ,
,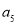 ,
, 成等差数列.
成等差数列.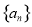 的通项公式及
的通项公式及 ;
;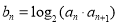 ,
,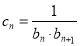 ,求数列
,求数列 的前
的前 项和
项和 .
. 如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.