题目内容
【题目】已知点P为曲线C上任意一点, ![]() ,直线
,直线![]() 、
、![]() 的斜率之积为
的斜率之积为![]() .
.
(Ⅰ)求曲线![]() 的轨迹方程;;
的轨迹方程;;
(Ⅱ)是否存在过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(I)设点![]() ,由
,由![]() ,整理得可得
,整理得可得![]() .
.
(II)设点![]() ,取MN的中点H,则
,取MN的中点H,则![]() ,则
,则![]() 可转化为
可转化为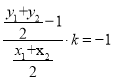 ,联立直线与椭圆,结合韦达定理建立关于斜率k的方程,求解即可.
,联立直线与椭圆,结合韦达定理建立关于斜率k的方程,求解即可.
试题解析:(I)设点![]() ,则
,则
![]()
整理得: ![]()
故曲线![]() 的轨迹方程为:
的轨迹方程为:
![]() .
.
(II)假设存在直线![]() 满足题意.
满足题意.
显然当直线斜率不存在时,直线与椭圆![]() 不相交.
不相交.
①当直线![]() 的斜率
的斜率![]() 时,设直线
时,设直线![]() 为:
为:![]()
联立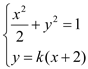 ,化简得:
,化简得:![]()
由![]() ,解得
,解得![]()
设点![]() ,
,![]() ,则
,则
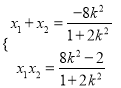
![]()
![]()
取![]() 的中点
的中点![]() ,则
,则![]() ,则
,则
即  ,化简得
,化简得![]() ,无实数解,故舍去.
,无实数解,故舍去.
②当![]() 时,
时, ![]() 为椭圆
为椭圆![]() 的左右顶点,显然满足
的左右顶点,显然满足![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() .
.
综上可知,存在直线![]() 满足题意,此时直线
满足题意,此时直线![]() 的方程为
的方程为![]() .
.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
【题目】随着城市化进程日益加快,劳动力日益向城市流动,某市为抽查该市内工厂的生产能力,随机抽取某个人数为1000人的工厂,其中有750人为高级工,250人为初级工,拟采用分层抽样的方法从本厂抽取100名工人,来抽查工人的生产能力,初级工和高级工的抽查结果分组情况如表1和表2.
表1:
生产能力分组 |
|
|
|
|
|
人数 | 4 | 8 |
| 5 | 3 |
表2:
生产能力分组 |
|
|
|
|
人数 | 6 |
| 36 | 18 |
(1)计算![]() ,
,![]() ,完成频率分直方图:
,完成频率分直方图:


图1:初级工人生产能力的频率分布直方图 图2:高级工人生产能力的频率分布直方图
(2)初级工和高级工各抽取多少人?
(3)分别估计两类工人生产能力的平均数,并估计该工厂工人生产能力的平均数.(同一组中的数据用该区间的中点值作代表)


