题目内容
【题目】如图，在三棱柱ABCA1B1C1中，AB AC，点E，F分别在棱BB1，CC1上（均异于端点），且∠ABE∠ACF，AE⊥BB1，AF⊥CC1．
求证：（1）平面AEF⊥平面BB1C1C；
（2）BC //平面AEF．
【答案】(1)证明见解析；(2)证明见解析.
【解析】试题分析：（1）在三棱柱
中， 
// 
，由
可推出
，再根据
，可证
平面
，从而可证平面
平面
；（2）根据
， 
， 
， 
，可证
≌
，结合（1），可推出四边形
是平行四边形，即可证明
//平面
．
试题解析：证明：（1）在三棱柱
中， 
// 
．
∵
∴
又∵
， 
， 
， 
平面
.
∴
平面
又∵
平面
∴平面
平面
（2）∵
， 
， 
， 
∴
≌
∴
又由（1）知， 
．
∴四边形
是平行四边形，从而
．
又∵
平面
， 
平面
∴
//平面
．
练习册系列答案
相关题目
【题目】根据消费者心理学的研究，商品的销售件数与购买人数存在一定的关系，商家可以根据此调整相应的商品小手策略，以谋求商品更多销量，从而获取更多利润.某商场对购买人数和销售件数进行了统计对比，得到如下表格：
人数 | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
件数 | 4 | 7 | 12 | 15 | 20 | 23 | 27 |
（参考公式：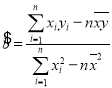
，
）
（1）以每天进店人数为横轴，每天商品销售件数为纵轴，画出散点图：
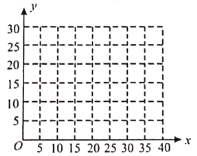
（2）根据（1）中所绘制的散点图，可得出购买人数与商品销售件数存在怎样的关系？并求出回归直线方程；（结果保留到小数点后两位）
（3）预测当进店人数为80人时，商品销售的件数.（结果保留整数）
