题目内容
6.若$|{\overrightarrow a}|=2,\overrightarrow b=({\sqrt{2},\sqrt{2}}),\overrightarrow a•({\overrightarrow b-\overrightarrow a})+2=0$,则向量$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{3}$.分析 设向量$\overrightarrow a$与$\overrightarrow b$的夹角为θ,先求出$\overrightarrow{a}$•$\overrightarrow{b}$=4cosθ,再根据向量的数量积即可求出
解答 解:设向量$\overrightarrow a$与$\overrightarrow b$的夹角为θ,
∵|$\overrightarrow{a}$|=2,$\overrightarrow{b}$=($\sqrt{2}$,$\sqrt{2}$),
∴|$\overrightarrow{b}$|=2,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=2×2×cosθ=4cosθ,
∵$\overrightarrow{a}$($\overrightarrow{b}$-$\overrightarrow{a}$)+2=0,
∴$\overrightarrow{a}$•$\overrightarrow{b}$-|$\overrightarrow{a}$|2+2=0,
∴cosθ=$\frac{1}{2}$,
∵0≤θ≤π,
∴θ=$\frac{π}{3}$,
故答案为:$\frac{π}{3}$.
点评 本题考查了向量的数量积的运算和向量的模因向量的夹角,属于基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
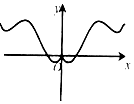
14.某多面体的三视图如下图所示(网格纸上小正方形的边长为1),则该多面体的表面积为( )

| A. | $8+4\sqrt{2}$ | B. | $6+4\sqrt{2}$ | C. | 12 | D. | $8+5\sqrt{2}$ |
11.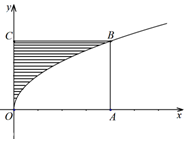 如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )
如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )
 如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )
如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )| A. | 2 | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
18.曲线y=x•ex在x=1处切线的斜率等于( )
| A. | 2e | B. | e | C. | 2 | D. | 1 |
15.已知向量$\overrightarrow a=(2cosθ,2sinθ),\overrightarrow b=(0,-2)$,$θ∈(\frac{π}{2},π)$,则向量夹角为( )
| A. | $\frac{3π}{2}-θ$ | B. | $θ-\frac{π}{2}$ | C. | $\frac{π}{2}+θ$ | D. | θ |