题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,且过点(-
,
).
(1)求椭圆C的标准方程;
(2)直线l与椭圆C相交于A、B两点,且|
+
| = |
|,求弦AB长度的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
(1)求椭圆C的标准方程;
(2)直线l与椭圆C相交于A、B两点,且|
| OA |
| OB |
| AB |
考点:直线与圆锥曲线的综合问题,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)利用椭圆C:
+
=1(a>b>0)的离心率为
,推出ab关系,化简椭圆方程,利用椭圆过点(-
,
).求解即可得到椭圆C的标准方程;
(2)利用|
+
| = |
|,推出
⊥
,通过直线l与x轴垂直求解线段的长度,直线l与不垂直,设出直线方程,与椭圆方程联立,通过数量积为0,结合弦长公式,即可求弦AB长度的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
(2)利用|
| OA |
| OB |
| AB |
| OA |
| OB |
解答:
解:(1)由e2=1-(
)2=
解得
=
,∴a=2b.
从而椭圆方程为
+
=1,
将(-
,
)代入得
+
=1,解得b2=1
∴b=1,a=2.∴椭圆方程为
+y2=1(3分)
(2)∵|
+
| = |
|∴
⊥
当l⊥x轴时,由对称性不妙设点A在第一象限,可求得A(
,
),B(
, -
)
∴|AB| =
=
当l不垂直于x轴时,可设直线l的方程为y=kx+m
由
消去y,得(1+4k2)x2+8kmx+4m2-4=0(4分)
由△=64k2m2-4(1+4k2)(4m2-4)>0得4k2+1>m2
设A(x1,y1),B(x2,y2),则x1+x2=-
, x1x2=
(5分)
∵
⊥
∴x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+km(x1+x2)+m2=0
代入得(1+k2) •
-km •
+m2=0,解得m2=
(7分)
∴|AB| =
|x1-x2|=
•
=
•
=
=
=
•
(9分)
=
•
=
当k=0时,|AB| =
当k≠0时,|AB| =
≤
=
且|AB| >
综上可知,弦AB长度的取值范围为[
,
](12分)
| b |
| a |
| 3 |
| 4 |
| b2 |
| a2 |
| 1 |
| 4 |
从而椭圆方程为
| x2 |
| 4b2 |
| y2 |
| b2 |
将(-
| 2 |
| ||
| 2 |
| 2 |
| 4b2 |
| 1 |
| 2b2 |
∴b=1,a=2.∴椭圆方程为
| x2 |
| 4 |
(2)∵|
| OA |
| OB |
| AB |
| OA |
| OB |
当l⊥x轴时,由对称性不妙设点A在第一象限,可求得A(
| 2 | ||
|
| 2 | ||
|
| 2 | ||
|
| 2 | ||
|
∴|AB| =
| 4 | ||
|
4
| ||
| 5 |
当l不垂直于x轴时,可设直线l的方程为y=kx+m
由
|
由△=64k2m2-4(1+4k2)(4m2-4)>0得4k2+1>m2
设A(x1,y1),B(x2,y2),则x1+x2=-
| 8km |
| 1+4k2 |
| 4m2-4 |
| 1+4k2 |
∵
| OA |
| OB |
代入得(1+k2) •
| 4m2-4 |
| 1+4k2 |
| 8km |
| 1+4k2 |
| 4k2+4 |
| 5 |
∴|AB| =
| 1+k2 |
| 1+k2 |
| (x1+x1)2-4x1x2 |
=
| 1+k2 |
| ||
| 1+4k2 |
| ||||
| 1+4k2 |
=
4
| ||||||
| 1+4k2 |
| 4 | ||
|
| ||
| 1+4k2 |
=
| 4 | ||
|
|
| 4 | ||
|
1+
|
当k=0时,|AB| =
| 4 | ||
|
当k≠0时,|AB| =
| 4 | ||
|
1+
|
| 4 | ||
|
1+
|
| 5 |
| 4 | ||
|
综上可知,弦AB长度的取值范围为[
4
| ||
| 5 |
| 5 |
点评:本题考查在与题意的综合应用,椭圆方程的求法,解题时注意直线是否与x轴垂直是解题的易疏忽点,考查分类讨论以及转化思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=3
的值域为( )
| 1 |
| x-1 |
| A、(0,+∞) |
| B、(0,1)∪(1,+∞) |
| C、{x|x≠1} |
| D、(1,+∞) |
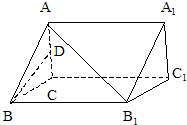 在空间平移正△ABC到△A1B1C1得到如图所示的几何体,若D是AC的中点,AA1⊥平面ABC,AA1:AB=
在空间平移正△ABC到△A1B1C1得到如图所示的几何体,若D是AC的中点,AA1⊥平面ABC,AA1:AB=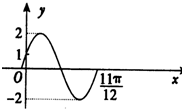 已知函数f(x)=A sin(ωx+ϕ)(A>0,ω>0,|φ|<
已知函数f(x)=A sin(ωx+ϕ)(A>0,ω>0,|φ|<