集合{α|α=$\frac{kπ}{2}$-$\frac{π}{5}$.k∈Z}∩{α|-π＜α＜π}为( )A．{-$\frac{π}{5}$.$\frac{3π}{10}$}B．{-$\frac{7π}{10}$.$\frac{4π}{5}$}C．{-$\frac{π}{5}$.-$\frac{7π}{10}$.$\frac{3π}{10}$.$\frac{4π}{5}$} 题目和参考答案——青夏教育精英家教网——

题目内容

3．集合{α|α=$\frac{kπ}{2}$-$\frac{π}{5}$，k∈Z}∩{α|-π＜α＜π}为（　　）

	A．	{-$\frac{π}{5}$，$\frac{3π}{10}$}		B．	{-$\frac{7π}{10}$，$\frac{4π}{5}$}
	C．	{-$\frac{π}{5}$，-$\frac{7π}{10}$，$\frac{3π}{10}$，$\frac{4π}{5}$}		D．	{$\frac{3π}{10}$，-$\frac{7π}{10}$}

分析只要解-π＜$\frac{kπ}{2}$-$\frac{π}{5}$＜π，对k取值即可．

解答解：由题意-π＜$\frac{kπ}{2}$-$\frac{π}{5}$＜π，解得-$\frac{8}{5}$＜k＜$\frac{12}{5}$，又k∈Z，所以k=-1，0，1，2，
所以集合{α|α=$\frac{kπ}{2}$-$\frac{π}{5}$，k∈Z}∩{α|-π＜α＜π}={-$\frac{π}{5}$，-$\frac{7π}{10}$，$\frac{3π}{10}$，$\frac{4π}{5}$}
故选：C．

点评本题考查了集合的运算，关键是确定k的取值，属于基础题．

练习册系列答案

学习指导与检测系列答案

高中学业水平测试卷系列答案

中考开卷考场指导用书考场制胜系列答案

奥数教程系列答案

百年学典金牌导学案系列答案

百思英语听力突破系列答案

百所名校专项期末卷系列答案

伴你学初中生生活系列答案

伴你学英语课堂活动手册系列答案

榜上有名中考新攻略系列答案

相关题目

13．我国从2016年1月1日起统一实施全面两孩政策．为了解适龄民众对放开生育二胎政策的态度，某市选取70后和80后作为调查对象，随机调查了100位，得到数据如表：

	生二胎	不生二胎	合计
70后	30	15	45
80后	45	10	55
合计	75	25	100

（1）以这100个人的样本数据估计该市的总体数据，且视频率为概率，若从该市70后公民中随机抽取3位，记其中生二胎的人数为X，求随机变量X的分布列，数学期望和方差；
（2）根据调查数据，是否有90%的把握认为“生二胎与年龄有关”，并说明理由．
参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
参考数据：

P（K²≥k₀）	0.15	0.10	0.05	0.025	0.010	0.005
k₀	2.072	2.706	3.841	5.024	6.635	7.879

14．设$\overrightarrow a，\overrightarrow b$均为单位向量，其夹角为θ，若$|\overrightarrow a+\overrightarrow b|＞1，|\overrightarrow a-\overrightarrow b|＞1$，则θ的取值范围为（$\frac{π}{3}$，$\frac{2π}{3}$）．

11．结合下面的算法：
第一步，输入x．
第二步，若x＜0，则y=x+3；否则，y=x-1．
第三步，输出y．
当输入的x的值为3时，输出的结果为2．

18．按照下列三种化合物的结构式及分子式的规律，归纳猜想出下一种化合物的分子式是（　　）

C₄H₉

C₄H₁₀

C₄H₁₁

C₆H₁₂

8．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的离心率为2，一个焦点与抛物线y²=16x的焦点相同，则双曲线的渐近线方程为（　　）

y=±$\frac{a}{2}$x

y=±$\frac{\sqrt{3}}{2}$x

y=±$\frac{\sqrt{3}}{3}$x

y=±$\sqrt{3}$x

15．对于数列{a_n}，定义${H_n}=\frac{{{a_1}+2{a_2}+…+{2^{n-1}}{a_n}}}{n}$为{a_n}的“优值”，现在已知某数列{a_n}的“优值”${H_n}={2^{n+1}}$，记数列{a_n-kn}的前n项和为S_n，若S_n≤S₅对任意的n∈N⁺恒成立，则实数k的最大值为$\frac{12}{5}$．

12．在△ABC中，角A，B，C的对边分别为a，b，c，已知cosC+cosAcosB=2cosAsinB．
（1）求tanA；
（2）若$b=2\sqrt{5}$，AB边上的中线$CD=\sqrt{17}$，求△ABC的面积．

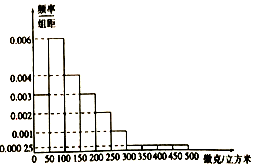根据环境保护部《环境空气质量指数（AQI）技术规定》，空气质量指数（AQI）在201-300之间为重度污染；在301-500之间为严重污染．依据空气质量预报，同时综合考虑空气污染程度和持续时间，将空气重污染分4个预警级别，由轻到重依次为预警四级、预警三级、预警二级、预警一级，分别用蓝、黄、橙、红颜色标示，预警一级（红色）为最高级别．（一）预警四级（蓝色）：预测未来1天出现重度污染；（二）预警三级（黄色）：预测未来1天出现严重污染或持续3天出现重度污染；（三）预警二级（橙色）；预测未来持续3天交替出现重度污染或严重污染；（四）预警一级（红色）；预测未来持续3天出现严重污染．
某城市空气质量监测部门对近300天空气中PM2.5浓度进行统计，得出这300天PM2.5浓度的频率分布直方图如图，将PM2.5浓度落入各组的频率视为概率，并假设每天的PM2.5浓度相互独立．
（1）求当地监测部门发布颜色预警的概率；
（2）据当地监测站数据显示未来4天将出现3天严重污染，求监测部门发布红色预警的概率．