题目内容
已知点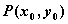
是椭圆
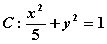上的一点。F1、F2是椭圆C 的左右焦点。
（1）若∠F1PF2是钝角，求点P 横坐标x0的取值范围；
（2）求代数式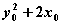
的最大值。
（1）
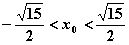（2）
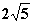
练习册系列答案
特高级教师点拨系列答案
相关题目
特高级教师点拨系列答案题目内容
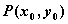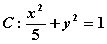已知点是椭圆上的一点。F1、F2是椭圆C 的左右焦点。
（1）若∠F1PF2是钝角，求点P 横坐标x0的取值范围；
（2）求代数式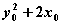的最大值。
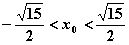（1） （2）
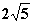
特高级教师点拨系列答案
的一元二次不等式
.
，
，则
的最大值为 
C．
D．
作一直线与椭圆
相交于A、B两点，若
点恰好为弦
的中点，则
且在两轴上截距相等的直线是（ ）
B. 
C. 
D.
或
-
中，
与平面ABCD所成角的余弦值为( )
B. 
C. 
D. 
上的一点
到椭圆一个焦点的距离为
，则
B 
D 
,
,
,那么角A等于 （ ）