题目内容
20.设函数$f(x)=a{x^2}-\frac{1}{2}-lnx$,曲线y=f(x)在x=2处与直线2x+3y=0垂直.(1)求函数f(x)的单调区间;
(2)当x>1时,证明f(x)>$\frac{1}{x}$-e1-x.
分析 (1)求出函数的对数,计算f′(2),求出a的值,求出函数的导数,求出函数的单调区间即可;
(2)令$g(x)=f(x)-(\frac{1}{x}-{{e}^{1-x}})$,由$\frac{1}{x}-{{e}^{1-x}}=\frac{{{{e}^{x-1}}-x}}{{x{{e}^{x-1}}}}$,令h(x)=ex-1-x,根据函数的单调性证明即可.
解答 解:(1)函数f(x)定义域为(0,+∞),$f'(x)=2ax-\frac{1}{x}$,…(2分)
由已知得$f'(2)=\frac{3}{2}$,所以$a=\frac{1}{2}$,…(3分)
所以$f'(x)=x-\frac{1}{x}=\frac{{{x^2}-1}}{x}$,由f'(x)>0得x>1,由f'(x)<0得0<x<1,
故函数f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1). …(5分)
(2)令$g(x)=f(x)-(\frac{1}{x}-{{e}^{1-x}})$,则$g'(x)=x-\frac{1}{x}+\frac{1}{x^2}-{{e}^{1-x}}$,…(6分)
由$\frac{1}{x}-{{e}^{1-x}}=\frac{{{{e}^{x-1}}-x}}{{x{{e}^{x-1}}}}$,令h(x)=ex-1-x,则h'(x)=ex-1-1,
当x>1时,h'(x)>0,所以h(x)在(1,+∞)上为增函数,
所以h(x)>h(1)=0,所以$\frac{1}{x}-{{e}^{1-x}}>0$,即:$-{{e}^{1-x}}>-\frac{1}{x}$,…(9分)
所以$g'(x)>x-\frac{2}{x}+\frac{1}{x^2}$,而$x-\frac{2}{x}+\frac{1}{x^2}=\frac{{{x^3}-2x+1}}{x^2}>\frac{{{x^2}-2x+1}}{x^2}>0$,
所以g'(x)>0,所以g(x)在(1,+∞)上为增函数,
所以g(x)>g(1)=0,即:$f(x)>\frac{1}{x}-{{e}^{1-x}}$ …(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道综合题.

| A. | 左上方 | B. | 左下方 | C. | 右上方 | D. | 右下方 |
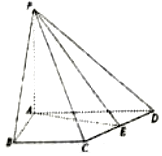 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB=∠ABC=90°,AB=4,BC=3,AD=5,E是CD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB=∠ABC=90°,AB=4,BC=3,AD=5,E是CD的中点.