题目内容
12.在平面直角坐标系xoy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,半圆C的极坐标方程为$ρ=2sinθ,θ∈[{0,\frac{π}{2}}]$.(1)求C的参数方程;
(2)设点D在C上,C在D处的切线与直线$l:x-\sqrt{3}y-2=0$垂直,根据(1)中的参数方程,确定点D的坐标.
分析 (1)先求出半圆C的直角坐标方程,由此能求出半圆C的参数方程.
(2)设点D对应的参数为α,则点D的坐标为(cosα,1+sinα),且α∈[-$\frac{π}{2},\frac{π}{2}$],半圆C的圆心是C(0,1)因半圆C在D处的发线与直线l垂直,故直线DC的斜率与直线l的斜率相等,由此能求出点D的坐标.
解答 解:(1)∵半圆C的极坐标方程为$ρ=2sinθ,θ∈[{0,\frac{π}{2}}]$.
即ρ2=2ρsinθ,$θ∈[0,\frac{π}{2}]$,
∴半圆C的直角坐标方程为x2+y2-2y=0,x∈[0,1],
∴半圆C的参数方程为$\left\{\begin{array}{l}{x=cosα}\\{y=1+sinα}\end{array}\right.,(α∈[-\frac{π}{2},\frac{π}{2}]为参数)$.
(2)设点D对应的参数为α,则点D的坐标为(cosα,1+sinα),且α∈[-$\frac{π}{2},\frac{π}{2}$],
由(1)知半圆C的圆心是C(0,1)
因半圆C在D处的发线与直线l垂直,故直线DC的斜率与直线l的斜率相等,
$\frac{(1+sinα)-1}{cosα}=\frac{\sqrt{3}}{3}$,即tanα=$\frac{\sqrt{3}}{3}$,
∵α∈[-$\frac{π}{2},\frac{π}{2}$],∴α=$\frac{π}{6}$,
∴点D的坐标为D($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
点评 本题考查参数方程的求法,考查点的坐标的求法,是中档题,解题时要认真审题,注意极坐标方程、直角坐标方程、参数方程的互化公式的合理运用.

练习册系列答案
相关题目
3.如图可能是下列哪个函数的图象( )
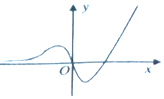

| A. | y=2x-x2-1 | B. | $y=\frac{{{2^x}sinx}}{4x+1}$ | C. | $y=\frac{x}{lnx}$ | D. | y=(x2-2x)ex |
4.“(x-1)(x-2)=0”是“x-1=0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |