题目内容
10.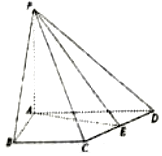 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB=∠ABC=90°,AB=4,BC=3,AD=5,E是CD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB=∠ABC=90°,AB=4,BC=3,AD=5,E是CD的中点.(1)证明:CD⊥平面PAE;
(2)若∠PBA=60°,求四棱锥P-ABCD的体积.
分析 (1)连接AC,推出CD⊥AE,PA⊥CD,然后证明CD⊥平面PAE.
(2)求出的底面面积以及高即可求解几何体的体积.
解答 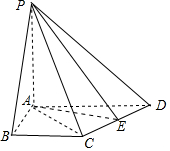 证明:(1)连接AC,由AB=4,BC=3,∠ABC=90°,得AC=5.
证明:(1)连接AC,由AB=4,BC=3,∠ABC=90°,得AC=5.
又AD=5,E是CD的中点,所以CD⊥AE.
∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD,
又PA∩AE=A,
所以CD⊥平面PAE.
(2)由已知可得$PA=4\sqrt{3}$,SABCD=16,$V=\frac{1}{3}×16×4\sqrt{3}=\frac{{64\sqrt{3}}}{3}$.
点评 本题考查直线与平面垂直的判定定理的应用,几何体的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
1.已知复数$z=\frac{5-i}{1-i}$,则z的虚部为( )
| A. | 2i | B. | 3i | C. | 2 | D. | 3 |
18.已知全集U={1,2,3,4,5,6},集合A={1,2,4},B={2,4,6},则A∩(∁UB)=( )
| A. | {1} | B. | {2} | C. | {4} | D. | {1,2} |
19.若f(x)=log3x,则f′(3)等于( )
| A. | $\frac{1}{3}$ | B. | ln 3 | C. | $\frac{1}{3ln3}$ | D. | $\frac{1}{ln3}$ |
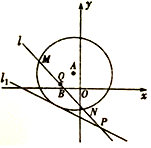 如图所示,已知圆A的圆心在直线y=-2x上,且该圆存在两点关于直线x+y-1=0对称,又圆A与直线l1:x+2y+7=0相切,过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
如图所示,已知圆A的圆心在直线y=-2x上,且该圆存在两点关于直线x+y-1=0对称,又圆A与直线l1:x+2y+7=0相切,过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.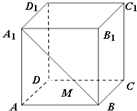 如图,棱长为1的正方体ABCD-A1B1C1D1中,M为线段A1B上的动点,则下列结论正确的有①②
如图,棱长为1的正方体ABCD-A1B1C1D1中,M为线段A1B上的动点,则下列结论正确的有①②