题目内容
20.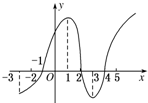 如图所示是y=f(x)的导数图象,则下列判断中正确结论的序号是②④.
如图所示是y=f(x)的导数图象,则下列判断中正确结论的序号是②④.①f(x)在(-3,1)上是增函数;
②x=-1是f(x)的极小值点;
③x=2是f(x)的极小值点;
④f(x)在(2,4)上是减函数,在(-1,2)上是增函数.
分析 根据图象求出函数的单调区间,从而求出函数的极值点,进而得到答案.
解答 解:由导函数的图象可得:
| x | (-3,-1) | -1 | (-1,2) | 2 | (2,4) | 4 | (4,+∞) |
| f′(x) | - | 0 | + | 0 | - | 0 | + |
| f(x) | 单减 | 极小 | 单增 | 极大 | 单减 | 极小 | 单增 |
②x=-1是f(x)的极小值点,正确;
③x=2是f(x)的极大值点,因此不正确.
④f(x)在区间(2,4)上是减函数,在区间(-1,2)上是增函数,正确;
综上可知:只有②④正确.
故答案为:②④
点评 本题考查了利用导函数的图象研究函数的单调性、极值等性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知集合P={0,x},Q={lnx,2},P∩Q={0},则P∪Q为( )
| A. | {0,2} | B. | {0,1,2} | C. | {1,2} | D. | {0,1} |
10.已知函数f(x)=$\left\{\begin{array}{l}xlnx-a{x^2},x≥1\\{a^x},x<1\end{array}$是减函数,则a的取值范围是( )
| A. | $(0,\frac{1}{2}]$ | B. | (0,1) | C. | $(\frac{1}{2},1)$ | D. | $[\frac{1}{2},1)$ |