题目内容
5.若q>0,命题甲:“a,b为实数,且|a-b|<2q”;命题乙:“a,b为实数,满足|a-2|<q,且|b-2|<q”,则甲是乙的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 根据充分必要条件的定义以及不等式的性质判断即可.
解答 解:若a,b为实数,且|a-b|<2q,
则-2q<a-b<2q,
故命题甲:-2q<a-b<2q;
若a,b为实数,满足|a-2|<q,且|b-2|<q,
则2-q<a<2+q①,2-q<b<2+q②,
由②得:-2-q<-b<-2+q③,
①+③得:-2q<a-b<2q,
故命题乙:-2q<a-b<2q,
故甲是乙的充分必要条件,
故选:C.
点评 本题考查了充分必要条件,考查不等式的性质,是一道基础题.

练习册系列答案
相关题目
15.sin(-1740°)的值是( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
16.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )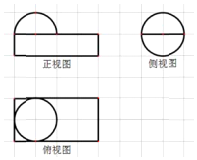

| A. | $\frac{14π}{3}$ | B. | $\frac{10π}{3}$ | C. | $\frac{8π}{3}$ | D. | $\frac{5π}{3}$ |
13.已知集合A={x|2x-1<0},B={x|0≤x≤1},那么A∩B等于( )
| A. | {x|x≥0} | B. | {x|x≤1} | C. | {x|0<x<$\frac{1}{2}$} | D. | {x|0≤x<$\frac{1}{2}$} |
10.已知z满足$({1-i})z=\sqrt{3}+i$(i为虚数单位),则|z|=( )
| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 2 | D. | 1 |
9.设全集U=R,集合A={x|x-1≤1},集合B={y|y=2x,x<1},则A∩(∁UB)=( )
| A. | {x|0<x<2} | B. | ∅ | C. | {0,2} | D. | {x|x≤0或x=2} |
