题目内容
已知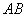 是圆柱底面圆的直径,
是圆柱底面圆的直径, 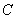 是底面圆周上异于
是底面圆周上异于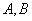 的任意一点,母线
的任意一点,母线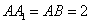 ;
;
(1)求证: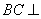 平面
平面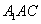 ;(2)求三棱锥
;(2)求三棱锥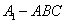 的体积的最大值.
的体积的最大值.
(1)∵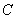 是底面圆周上异于
是底面圆周上异于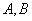 的任意一点,
的任意一点,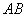 是圆柱底面圆的直径,
是圆柱底面圆的直径,
∴BC⊥AC, ∵AA1⊥平面ABC,BCÌ平面ABC,∴AA1⊥BC,
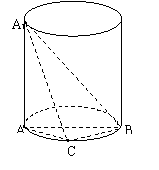 ∵AA1∩AC=A,AA1Ì平面AA1 C,ACÌ平面AA1 C,
∵AA1∩AC=A,AA1Ì平面AA1 C,ACÌ平面AA1 C,
∴BC⊥平面AA1C.
(2)解法1:设AC=x,在Rt△ABC中,
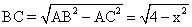 (0<x<2)
(0<x<2)
故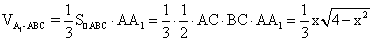 (0<x<2),
(0<x<2),
即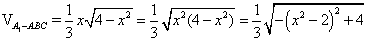 .
.
∵0<x<2,0<x2<4,∴当x2=2,即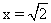 时,三棱锥A1-ABC的体积的最大值为
时,三棱锥A1-ABC的体积的最大值为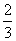
.解法2: 在Rt△ABC中,AC2+BC2=AB2=4,
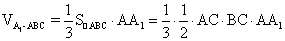
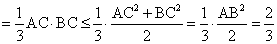 .
.
当且仅当 AC=BC 时等号成立,此时AC=BC=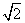 .
.
解法3:设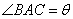 ,则在Rt△ABC中,
,则在Rt△ABC中,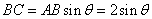 ,
,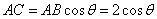
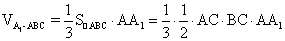
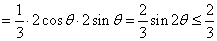 .
.
当且仅当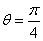 即 AC=BC 时等号成立,此时AC=BC=
即 AC=BC 时等号成立,此时AC=BC=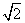 .
.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 在
在 上是增函数,则实数
上是增函数,则实数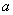 的取值范围是 .
的取值范围是 .
 的半圆面,则该圆锥的体积为 .
的半圆面,则该圆锥的体积为 .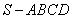 中,
中, ,那么当该棱锥的体积取最大时,高为 .
,那么当该棱锥的体积取最大时,高为 .  ,侧棱长为
,侧棱长为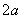 ,点
,点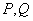 分别在
分别在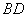 和
和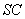 上,并且
上,并且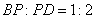 ,
,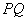 ∥平面
∥平面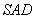 ,求线段
,求线段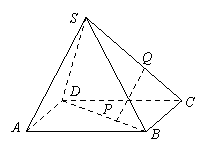
 与直线y=k(x-2)+4有两个不同交点,则实数k的取值范围是____.
与直线y=k(x-2)+4有两个不同交点,则实数k的取值范围是____.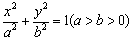 的离心率为
的离心率为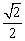 , 过点
, 过点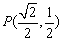 , 记椭圆的左顶点为
, 记椭圆的左顶点为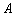 .
.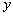 轴的直线
轴的直线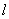 交椭圆于
交椭圆于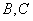 两点, 试求
两点, 试求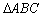 面积的最大值;
面积的最大值;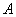 作两条斜率分别为
作两条斜率分别为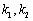 的直线交椭圆于
的直线交椭圆于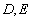 两点,且
两点,且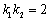 , 求证: 直线
, 求证: 直线 恒过一个定点.
恒过一个定点.
 从小到大排列为________.
从小到大排列为________.