题目内容
给出下列四个命题,正确命题的序号是
①函数y=tanx的图象关于点(
,0),k∈z对称
②函数y=sin|x|是最小正周期为π的周期函数
③设θ是第二象限角,则tan
>cos
且sin
>cos
④y=cos2x+sinx的最小值为-1.
①函数y=tanx的图象关于点(
| kπ |
| 2 |
②函数y=sin|x|是最小正周期为π的周期函数
③设θ是第二象限角,则tan
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
④y=cos2x+sinx的最小值为-1.
考点:正切函数的图象,命题的真假判断与应用
专题:综合题,三角函数的图像与性质
分析:根据正切函数的性质判断①;周期函数的定义判断②的正误;取特殊角判断③;根据正弦函数的性质判断④,即可推出结果.
解答:
解:①根据正切函数的图象可知,函数y=tanx图象关于点(
,0),(k∈z)对称,所以正确;
②函数y=sin|x|是偶函数,不是周期函数,故不正确;
③θ=480°时,结论不成立,故不正确;
④cos2x+sinx=-sin2x+sinx+1=-(sinx-
)2+
.因为x∈R,所以sinx∈[-1,1],当sinx=-1时,函数y=cos2x+sinx取得最小值-1,故正确.
故答案为:①④.
| kπ |
| 2 |
②函数y=sin|x|是偶函数,不是周期函数,故不正确;
③θ=480°时,结论不成立,故不正确;
④cos2x+sinx=-sin2x+sinx+1=-(sinx-
| 1 |
| 2 |
| 5 |
| 4 |
故答案为:①④.
点评:本题考查三角函数的周期性及其求法,正弦函数的对称性,正切函数的单调性,考查基本概念的掌握程度,是基础题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
投掷两枚骰子,所得点数之和记为X,那么X=4表示的随机实验结果是( )
| A、一枚是3点,一枚是1点 |
| B、一枚是3点,一枚是1点或两枚都是2点 |
| C、两枚都是4点 |
| D、两枚都是2点 |
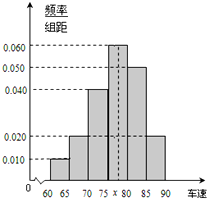 2014年“五一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图所示的频率分布直方图.若从车速在[60,70)的车辆中任抽取2辆,则车速在[65,70)的车辆至少有一辆的概率
2014年“五一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图所示的频率分布直方图.若从车速在[60,70)的车辆中任抽取2辆,则车速在[65,70)的车辆至少有一辆的概率