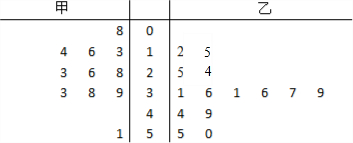
题目内容
设数列{an}满足:a1=1,a2=2,an+2=
n∈N).
(1)求an+1与an之间的递推关系式an+1=f(an);
(2)求证:当n≥2时,2<an2-an-12≤3;
(3)求a2014的整数部分.
| an(an+12+1) |
| an2+1 |
(1)求an+1与an之间的递推关系式an+1=f(an);
(2)求证:当n≥2时,2<an2-an-12≤3;
(3)求a2014的整数部分.
考点:数列递推式,数列的求和
专题:综合题,等差数列与等比数列
分析:(1)由an+2=
,可得
=
=…=
=1,即可得出an+1与an之间的递推关系;
(2)证明数列{an}是递增数列,an2-an-12=
-2,即可证明结论;
(3)a20142=
+
+…+
-2(2014-1),再进行放缩,即可求出a2014的整数部分.
| an(an+12+1) |
| an2+1 |
| an+2 | ||
an+1-
|
| an+1 | ||
an-
|
| 2 | ||
1-
|
(2)证明数列{an}是递增数列,an2-an-12=
| 1 |
| an-12 |
(3)a20142=
| 1 |
| a20132 |
| 1 |
| a20122 |
| 1 |
| a12 |
解答:
(1)解:由an+2=
,可得
=
,
∴
=
=…=
=1,
∴an+1=an-
;
(2)证明:∵a1=1,an+1=an-
,
∴数列{an}是递增数列,
∴0<
≤1,
n≥2时,an2=(an-1-
)2=an-12+
-2,
∴an2-an-12=
-2,
∴2<an2-an-12≤3;
(3)解:∵an2=an-12+
-2,
∴a20142=
+
+…+
-2(2014-1)
∵n≥3时,an2>2n,
∴a20142<4026+1+
+…+
=4027+
[(
+
+…+
)+(
+…+
)+(
+…+
)]
<4027+
(
×38+
×160+
×1814)
<4027+
(19+4+10)<4096=642,
∴63<a2014<64,
∴a2014的整数部分为63.
| an(an+12+1) |
| an2+1 |
| an+2 | ||
an+1-
|
| an+1 | ||
an-
|
∴
| an+2 | ||
an+1-
|
| an+1 | ||
an-
|
| 2 | ||
1-
|
∴an+1=an-
| 1 |
| an |
(2)证明:∵a1=1,an+1=an-
| 1 |
| an |
∴数列{an}是递增数列,
∴0<
| 1 |
| an2 |
n≥2时,an2=(an-1-
| 1 |
| an-1 |
| 1 |
| an-12 |
∴an2-an-12=
| 1 |
| an-12 |
∴2<an2-an-12≤3;
(3)解:∵an2=an-12+
| 1 |
| an-12 |
∴a20142=
| 1 |
| a20132 |
| 1 |
| a20122 |
| 1 |
| a12 |
∵n≥3时,an2>2n,
∴a20142<4026+1+
| 1 |
| 4 |
| 1 |
| 2×2013 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 39 |
| 1 |
| 40 |
| 1 |
| 199 |
| 1 |
| 200 |
| 1 |
| 2013 |
<4027+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 40 |
| 1 |
| 200 |
<4027+
| 1 |
| 2 |
∴63<a2014<64,
∴a2014的整数部分为63.
点评:本题考查数列递推式,考查数列与不等式的综合,考查学生分析解决问题的能力,有难度.

练习册系列答案
相关题目
设f(x)=x(x-1)(x-2)…(x-1000),则f′(0)=( )
| A、501! | B、500! |
| C、-1000! | D、1000! |
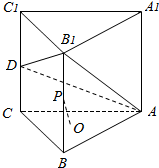 三棱柱ABC-A1B1C1中,点D、P为棱CC1、BB1的中点,O为△ABC重心,求证:OP∥平面AB1D.
三棱柱ABC-A1B1C1中,点D、P为棱CC1、BB1的中点,O为△ABC重心,求证:OP∥平面AB1D.