题目内容
斜率为1的直线L经过抛物线y2=2x的焦点,与抛物线相交于A,B两点,则|AB|= .
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:求出抛物线y2=2x的焦点F,准线方程,由题意可得直线AB的方程,代入抛物线方程,根据方程的根与系数的关系,结合抛物线的定义可求线段AB的长.
解答:
解:抛物线y2=2x的焦点F(
,0),准线方程为x=-
,
∴直线AB的方程为y=x-
,代入抛物线方程可得x2-3x+
=0
∴xA+xB=3,
由抛物线的定义可知,|AB|=|AF|+|BF|=xA+
+xB+
=xA+xB+1=4
故答案为:4.
| 1 |
| 2 |
| 1 |
| 2 |
∴直线AB的方程为y=x-
| 1 |
| 2 |
| 1 |
| 4 |
∴xA+xB=3,
由抛物线的定义可知,|AB|=|AF|+|BF|=xA+
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:4.
点评:本题主要考查了直线与抛物线的位置关系:相交关系的应用,方程的根系数的关系的应用,主要体现了抛物线的定义的灵活应用.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知抛物线y2=2px过点 A(1,2),设抛物线的焦点为F,则|FA|等于( )
| A、6 | B、7 | C、5 | D、2 |
以-3i+
的虚部为实部,以-3i2+
i的实部为虚部的复数是( )
| 2 |
| 2 |
| A、3-3i | ||||
| B、-3+3i | ||||
C、-
| ||||
D、
|
等比数列{an}中,a6=2,a5=5,则数列{lgan}的前10项和等于( )
| A、6 | B、5 | C、4 | D、3 |
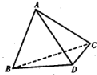 四面体ABCD中,△ABC是正三角形,△BCD是等腰直角三角形,其中BD=DC=
四面体ABCD中,△ABC是正三角形,△BCD是等腰直角三角形,其中BD=DC=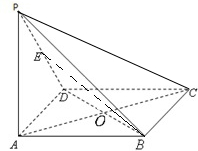 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=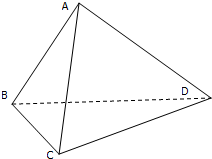 如图所示,空间四边形ABCD中,平面ABD⊥平面BCD,∠BAD=90°,∠BCD=90°,且AB=AD,则AC与平面BCD所成的角为
如图所示,空间四边形ABCD中,平面ABD⊥平面BCD,∠BAD=90°,∠BCD=90°,且AB=AD,则AC与平面BCD所成的角为