题目内容
如图,已知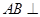 平面
平面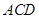 ,
,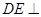 平面
平面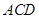 ,△
,△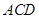 为等边三角形,
为等边三角形,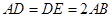 ,
,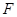 为
为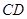 的中点.
的中点.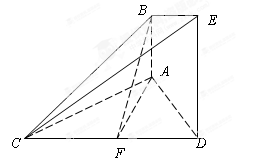
(1)求证: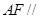 平面
平面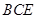 ;
;
(2)求证:平面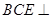 平面
平面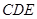 ;
;
(3)求直线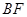 和平面
和平面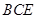 所成角的正弦值.
所成角的正弦值.
(1)证 (2)证
(2)证 平面
平面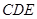 (3)
(3)
解析试题分析:(1)证法一:取 的中点
的中点 ,连
,连 .
.
∵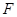 为
为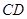 的中点,∴
的中点,∴ 且
且 .
.
∵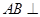 平面
平面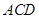 ,
,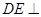 平面
平面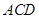 ,
,
∴ ,∴
,∴ .
.
又 ,∴
,∴ .
.
∴四边形 为平行四边形,则
为平行四边形,则 .
.
∵ 平面
平面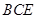 ,
, 平面
平面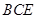 ,
,
∴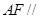 平面
平面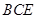 .
.
(2)证:∵ 为等边三角形,
为等边三角形,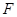 为
为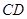 的中点,
的中点,
∴ .
.
∵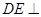 平面
平面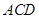 ,
, 平面
平面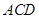 ,∴
,∴ .
.
又 ,故
,故 平面
平面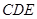 .
.
∵ ,∴
,∴ 平面
平面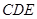 .
.
∵ 平面
平面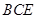 ,
,
∴平面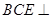 平面
平面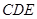 .
.
(3)解:在平面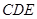 内,过
内,过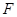 作
作 于
于 ,连
,连 .
.
∵平面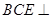 平面
平面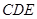 ,∴
,∴ 平面
平面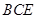 .
.
∴ 为
为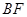 和平面
和平面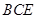 所成的角.
所成的角.
设 ,则
,则 ,
, ,
,
R t△ 中,
中, .
.
∴直线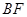 和平面
和平面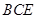 所成角的正弦值为
所成角的正弦值为 .
.
考点:平面与平面垂直的判定;直线与平面平行的判定;直线与平面所成的角.
点评:本题考查证明线面平行的方法,2个平面垂直的方法,求直线与平面成的角的方法,属于中档题.

练习册系列答案
相关题目

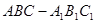 的三视图如图所示,
的三视图如图所示,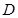 是
是 的中点.
的中点.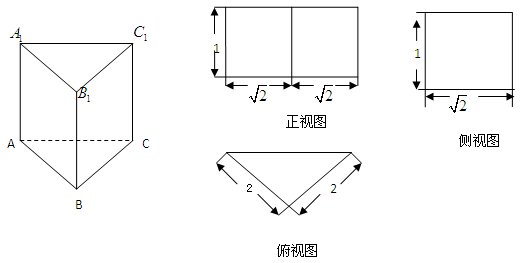
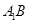 ∥平面
∥平面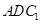 ;
;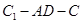 的余弦值;
的余弦值;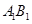 上是否存在点
上是否存在点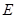 ,使
,使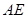 与
与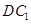 成
成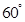 角?若存在,确定
角?若存在,确定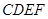 为正方形,面
为正方形,面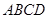 为等腰梯形,
为等腰梯形,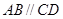 ,
,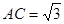 ,
,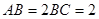 ,
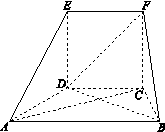
,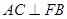 .
.
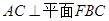 ;
;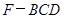 的体积;
的体积; 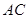 上是否存在点
上是否存在点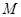 ,使
,使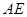 //平面
//平面 ?证明你的结论.
?证明你的结论.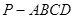 中,
中,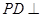 底面
底面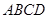 ,面
,面 为侧棱
为侧棱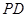 上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
上一点.该四棱锥的俯视图和侧(左)视图如图2所示. 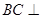 平面
平面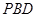 ;
; 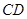 上是否存在点
上是否存在点 ,使
,使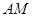 与
与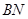 所成角的余弦值为
所成角的余弦值为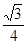 ?若存在,找到所有符合要求的点
?若存在,找到所有符合要求的点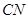 的长;若不存在,说明理由.
的长;若不存在,说明理由.
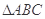 是等腰直角三角形,其中
是等腰直角三角形,其中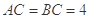 ,
,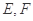 分别为
分别为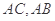 的中点,将
的中点,将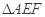 沿
沿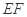 折起,点
折起,点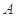 的位置变为点
的位置变为点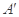 ,已知点
,已知点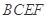 上的射影
上的射影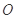 为
为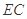 的中点,如图(2)所示.
的中点,如图(2)所示.
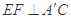 ;
;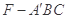 的体积.
的体积. 平面ABCD,
平面ABCD, ,E是PC上的一点.
,E是PC上的一点.
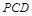 ;
;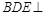 平面
平面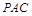 ;
; 为多长时,
为多长时, 平面
平面 ?
? 中,
中,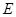 是
是 的中点.
的中点.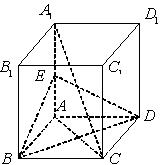
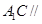 平面
平面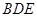 ;
;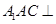 平面
平面