题目内容
边长为2的正方形ABCD所在平面外有一点P, 平面ABCD,
平面ABCD, ,E是PC上的一点.
,E是PC上的一点.
(Ⅰ)求证:AB//平面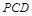 ;
;
(Ⅱ)求证:平面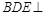 平面
平面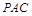 ;
;
(Ⅲ)线段 为多长时,
为多长时, 平面
平面 ?
?
(1)利用直线与平面平行的判定定理直接证明AB∥平面PCD.
( 2)通过证明PA⊥BD,结合PA∩AC=A,推出BD⊥平面PAC,然后证明平面BDE⊥平面PAC.
( 3)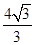
解析试题分析:解:(Ⅰ)证明:正方形ABCD中, AB//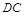 ,又AB
,又AB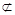 平面
平面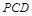 ,
,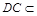 平面
平面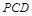
所以AB//平面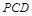 3分
3分
(Ⅱ)证明:正方形ABCD中,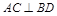 ,
,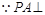 平面ABCD,
平面ABCD,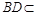 平面ABCD,
平面ABCD,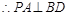 , 5分
, 5分
又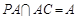 ,所以
,所以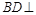 平面
平面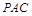 , 6分
, 6分 平面
平面 ,
,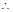 平面
平面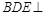 平面
平面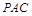 8分
8分
(Ⅲ)由(Ⅱ)可知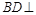
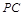 ,所以只需
,所以只需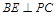 可证
可证 平面
平面 ,
,
在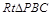 中,可求
中,可求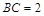 ,
,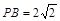 ,
, ,
,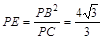 12分
12分
考点:直线与平面平行,面面垂直
点评:本题考查直线与平面平行,平面与平面垂直的证明,考查空间想象能力.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
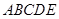 中,
中,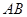 ⊥平面
⊥平面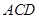 ,
,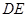 ⊥平面
⊥平面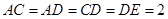 ,
,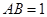 ,
,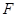 为
为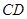 的中点.
的中点.
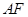 ⊥平面
⊥平面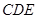 ;
;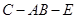 的大小.
的大小.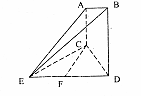
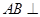 平面
平面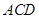 ,
,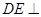 平面
平面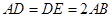 ,
,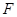 为
为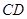 的中点.
的中点.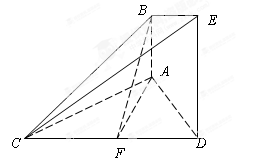
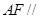 平面
平面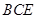 ;
;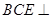 平面
平面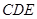 ;
;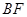 和平面
和平面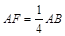 .
.
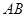 是半圆
是半圆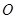 的直径,
的直径, 是半圆
是半圆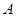 、
、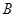 外的一个动点,
外的一个动点,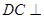 平面
平面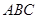 ,
,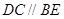 ,
,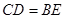 ,
,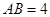 ,
,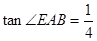 .
.
 平面
平面 ;
;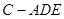 的体积取得最大值,请说明理由并求出这个最大值.
的体积取得最大值,请说明理由并求出这个最大值.
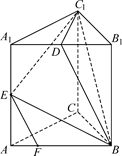
 是正三角形,AB
是正三角形,AB 平面BCD,
平面BCD, ,E为BC的中点,F在棱AC上,且
,E为BC的中点,F在棱AC上,且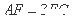

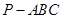 中,
中,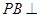 底面
底面 于
于 ,
, ,
, ,点
,点 是
是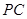 的中点.
的中点.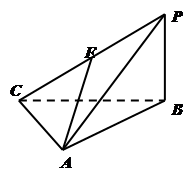
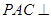 平面
平面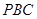 ;
;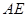 与
与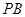 所成的角为
所成的角为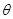 ,且
,且 ,
,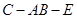 的大小.
的大小.