题目内容
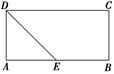
如图(1),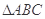 是等腰直角三角形,其中
是等腰直角三角形,其中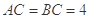 ,
,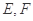 分别为
分别为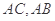 的中点,将
的中点,将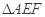 沿
沿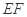 折起,点
折起,点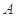 的位置变为点
的位置变为点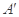 ,已知点
,已知点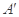 在平面
在平面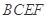 上的射影
上的射影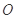 为
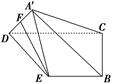
为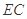 的中点,如图(2)所示.
的中点,如图(2)所示.
(1)求证: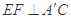 ;
;
(2)求三棱锥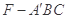 的体积.
的体积.
(1)根据题意,由于题目中可以得到线面垂直,结合其性质定理来得到线线垂直。
(2)
解析试题分析:
解:(1)证法一:在 中,
中,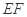 是等腰直角
是等腰直角 的中位线,
的中位线,
在四棱锥 中,
中, ,
, ,
,  平面
平面 ,
,
又 平面
平面 ,
,  6分
6分
证法二:同证法一

 平面
平面 ,
,
又 平面
平面 ,
,  6分
6分
(2)在直角梯形 中 ,
中 , ,
, 
 =
=
又 垂直平分
垂直平分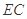 ,
, 9分
9分 三棱锥
三棱锥 的体积为:
的体积为: 12分
12分
考点:线面垂直,锥体的体积
点评:主要是考查了空间中线线垂直的证明以及三棱锥的体积的求解,,属于中档题。

练习册系列答案
相关题目
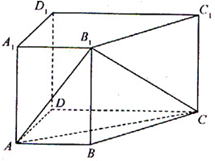
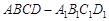 中,侧棱
中,侧棱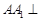 底面
底面 ,
,
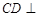 平面
平面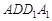
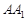 与平面
与平面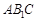 所成角的正弦值为
所成角的正弦值为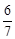 ,求
,求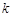 的值
的值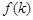 ,写出
,写出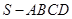 的底面
的底面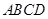 是直角梯形,
是直角梯形,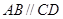 ,
,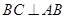 ,侧面
,侧面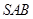 为正三角形,
为正三角形,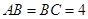 ,
,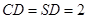 .如图所示.
.如图所示.
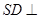 平面
平面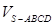 .
. 的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=
的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=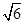 ,M,N分别为PB,PD的中点.
,M,N分别为PB,PD的中点.
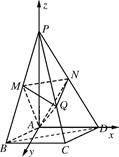
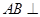 平面
平面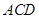 ,
,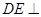 平面
平面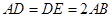 ,
,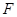 为
为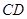 的中点.
的中点.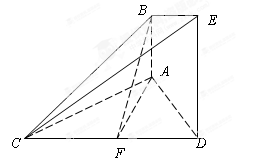
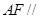 平面
平面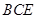 ;
;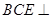 平面
平面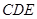 ;
;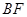 和平面
和平面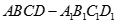 ,
, 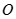 是底
是底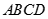 对角线的交点.
对角线的交点.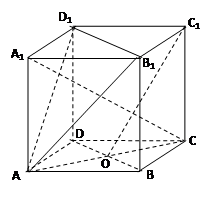
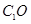 ∥面
∥面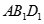 ;
;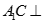 面
面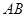 是半圆
是半圆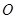 的直径,
的直径, 是半圆
是半圆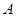 、
、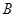 外的一个动点,
外的一个动点,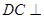 平面
平面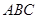 ,
,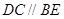 ,
,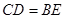 ,
,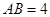 ,
,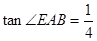 .
.
 平面
平面 ;
;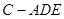 的体积取得最大值,请说明理由并求出这个最大值.
的体积取得最大值,请说明理由并求出这个最大值. 的底面是正方形,
的底面是正方形, ,点
,点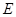 在棱
在棱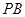 上.
上.
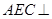 平面
平面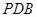 ;
;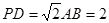 ,且
,且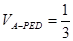 时,确定点
时,确定点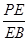 的值.
的值.