题目内容
已知数列{an}的前n项和为Sn,且2Sn=3an-1.
(1)求数列{an}的通项公式;
(2)令bn=nan,求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)令bn=nan,求数列{bn}的前n项和Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)利用n=1时,a1=S1,当n≥2时,an=Sn-Sn-1即可得出;
(2)利用“错位相减法”,等比数列的前n项和公式即可得出.
(2)利用“错位相减法”,等比数列的前n项和公式即可得出.
解答:
解:(1)n=1时,a1=1.
∵2Sn=3an-1,∴2Sn+1=3an+1-1,
∴an+1=3an,
∴an=3n-1.
(2)∵bn=n?3n-1,
∴Tn=1?30+2?31+3?32+…+(n-1)?3n-2+n?3n-1,
3 Tn=1?31+2?32+3?33+…+(n-1)?3n-1+n?3n,
两式相减可得-2Tn=1+31+32+…+3n-1-n?3n,
∴Tn=
?3n+
.
∵2Sn=3an-1,∴2Sn+1=3an+1-1,
∴an+1=3an,
∴an=3n-1.
(2)∵bn=n?3n-1,
∴Tn=1?30+2?31+3?32+…+(n-1)?3n-2+n?3n-1,
3 Tn=1?31+2?32+3?33+…+(n-1)?3n-1+n?3n,
两式相减可得-2Tn=1+31+32+…+3n-1-n?3n,
∴Tn=
| 2n-1 |
| 4 |
| 1 |
| 4 |
点评:本题考查了递推式的应用、等比数列的通项公式及其前n项和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
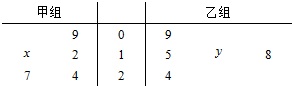 以下茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).
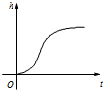
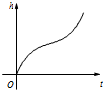
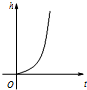
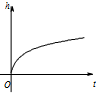
以下茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).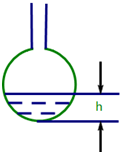 匀速地向下部是球形、上部是圆柱形的容器(如图所示)内注水,那么注水时间t与容器内水的高度h之间的函数关系 h=f(t)的图象大致是下图中的( )
匀速地向下部是球形、上部是圆柱形的容器(如图所示)内注水,那么注水时间t与容器内水的高度h之间的函数关系 h=f(t)的图象大致是下图中的( )