题目内容
4．集合{x||x-1|＜3，且x∈N}的真子集个数为（ ）| A． | 15 | B． | 16 | C． | 31 | D． | 32 |
分析 利用列举法表示出集合，再利用含有n个元素的集合，它的子集共有2n个，它的真子集共有2n-1，从而得出结论．
解答 解：集合{x||x-1|＜3，且x∈N}={x|-2＜x＜4，x∈N}={0，1，2，3}，
故集合中共计含有4个元素，故它的真子集的个数为24-1=15，
故选：A．
点评 本题主要考查集合的表示法，利用了含有n个元素的集合，它的子集共有2n个，它的真子集共有2n-1个，属于基础题．
练习册系列答案
相关题目
14．已知a，b是两条直线，α是一个平面，则下列判断正确的是（ ）
| A． | a⊥α，b⊥α，则a⊥b | B． | a∥α，b?α，则a∥b | C． | a⊥b，b?α，则a⊥α | D． | a∥α，b?α，则a∥α |
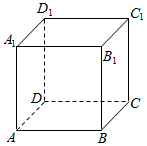在正方体ABCD-A1B1C1D1中，求下列异面直线所成角的大小