题目内容
已知数列 的前n项和为
的前n项和为 ,并且满足
,并且满足 .
.
(1)求数列 的通项公式
的通项公式 ;
;
(2)设 为数列
为数列 的前n项和,求
的前n项和,求 ;
;
(3)设 ,证明:
,证明:
解:(1)当 时,∵
时,∵ ①,
①,
∴ ②,……………………………1分
②,……………………………1分
两式相减得
即 ,……………………………2分
,……………………………2分
∵
所以数列 是公差为2的等差数列。……………………………3分
是公差为2的等差数列。……………………………3分
∴ ,当
,当 时也满足上式,
时也满足上式,
∴数列 的通项公式为
的通项公式为 .……………………………4分
.……………………………4分
(2)∵
∴ ③, ③式两边同时乘以
③, ③式两边同时乘以 得,
得,
 ④,……………………………5分
④,……………………………5分
③-④得  ……………………………7分
……………………………7分
即 .……………………………8分
.……………………………8分
(3)∵ ,……………………………9分
,……………………………9分
∴
 ……………………………10分
……………………………10分
 .……………………………12分
.……………………………12分

练习册系列答案
相关题目

 与圆
与圆 交于
交于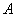 、
、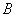 两点,则
两点,则 的面积为 .
的面积为 .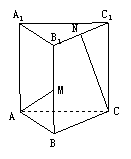 如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M、N分别是BB1和B1C1的中点,则直线AM与CN所成角的余弦值等于( )
如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M、N分别是BB1和B1C1的中点,则直线AM与CN所成角的余弦值等于( )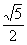 B.
B.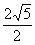 C.
C.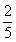 D.
D.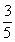
 是公差不为
是公差不为 的等差数列,
的等差数列, 且
且 、
、 、
、 成等比数列,则
成等比数列,则 项和
项和 ( )
( ) B.
B. C.
C.  D.
D. 
 、
、 满足约束条件
满足约束条件 ,则
,则 的最大值为_________.
的最大值为_________. .
. 时,
时, ,求a的取值范围;
,求a的取值范围; ,
, 恒成立,求实数a的最小值.
恒成立,求实数a的最小值. 的焦点
的焦点 ,该抛物线上的一点
,该抛物线上的一点 到
到 轴的距离为3,则
轴的距离为3,则

 C.
C. 若
若 则
则

 (k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2015年生产该产品的固定投入为8万元.每生产一万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2015年生产该产品的固定投入为8万元.每生产一万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).